题目内容
已知函数f(x)=x3+
(x∈R),f(x1)+f(x2)>0,则下列不等式中正确的是( )
| 2x-1 |
| 2x+1 |
| A、x1>x2 |
| B、x1<x2 |
| C、x1+x2>0 |
| D、x1+x2<0 |
考点:利用导数研究函数的单调性,不等关系与不等式
专题:函数的性质及应用
分析:先判定函数f(x)的奇偶性与单调性,即可得出.
解答:
解:f(x)=x3+1-
,
由于函数y=2x在R单调递增,∴函数y=
在R上单调递减,∴函数y=-
在R上单调递增.
又函数y=x3在R上单调递增.
∴函数f(x)在R上单调递增.
又f(-x)=-x3+
=-x3+
=-f(x).
∴函数f(x)在R上为奇函数.
∵f(x1)+f(x2)>0,
∴f(x1)>-f(x2)=f(-x2),
∴x1>-x2,
∴x1+x2>0,
故选:C.
| 2 |
| 2x+1 |
由于函数y=2x在R单调递增,∴函数y=
| 1 |
| 2x+1 |
| 2 |
| 2x+1 |
又函数y=x3在R上单调递增.
∴函数f(x)在R上单调递增.
又f(-x)=-x3+
| 2-x-1 |
| 2-x+1 |
| 1-2x |
| 1+2x |
∴函数f(x)在R上为奇函数.
∵f(x1)+f(x2)>0,
∴f(x1)>-f(x2)=f(-x2),
∴x1>-x2,
∴x1+x2>0,
故选:C.
点评:本题考查了函数的奇偶性与单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
当x∈(0,
)时,下面四个函数中最大的是( )
| π |
| 4 |
| A、sin(cosx) |
| B、sin(sinx) |
| C、cos(sinx) |
| D、cos(cosx) |
某2列联表为:
则x与y之间有关系的可能性为( )
| y1 | y2 | |
| x1 | 5 | 15 |
| x2 | 40 | 10 |
| A、0.1% | B、99.9% |
| C、97.5% | D、0.25% |
若函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω和φ的取值是( )
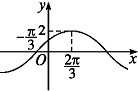

A、ω=
| ||||
B、ω=
| ||||
C、ω=1,φ=-
| ||||
D、ω=1,φ=
|
若a<b<0,则下列不等关系中,不能成立的是( )
A、
| ||||
B、
| ||||
C、a
| ||||
D、a
|
已知数列{an}共有2n+1项,其中奇数项通项公式为an=2n-1,则数列{an}的奇数项的和为( )
| A、2(2n+1-1)-n-1 | ||
B、
| ||
| C、2(4n+1-1)-n-1 | ||
D、
|
已知椭圆准线x=4对应焦点(2,0),离心率e=
,则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
| B、3x2+y2+28y+60=0 | ||||
| C、3x2+4y2-8x=0 | ||||
| D、2x2+3y2-7x+4=0 |
集合{a,b,c,d}的子集有( )
| A、4个 | B、8个 |
| C、16个 | D、32个 |
若a>b,则下列不等式中恒成立的是( )
A、
| ||||
B、
| ||||
| C、a2>b2 | ||||
| D、a3>b3 |