题目内容
函数y=sin2(
+x)-sin2(
-x)的值域是( )
| π |
| 4 |
| π |
| 4 |
| A、[-1,0] | ||
| B、[0,1] | ||
| C、[-1,1] | ||
D、[-
|
考点:二倍角的余弦
专题:三角函数的图像与性质
分析:由y=sin2(
+x)-sin2(
-x)=
-
=sin2x,能求出函数y=sin2(
+x)-sin2(
-x)的值域.
| π |
| 4 |
| π |
| 4 |
1-cos(
| ||
| 2 |
1-cos(
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:∵y=sin2(
+x)-sin2(
-x)
=
-
=
-
=sin2x,
∴函数y=sin2(
+x)-sin2(
-x)的值域是[-1,1].
故选:C.
| π |
| 4 |
| π |
| 4 |
=
1-cos(
| ||
| 2 |
1-cos(
| ||
| 2 |
=
| 1+sin2x |
| 2 |
| 1-sin2x |
| 2 |
=sin2x,
∴函数y=sin2(
| π |
| 4 |
| π |
| 4 |
故选:C.
点评:本题考查三角函数的值域的求法,是基础题,解题时要认真审题,注意二倍角的余弦公式的合理运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
若a<b<0,则下列不等关系中,不能成立的是( )
A、
| ||||
B、
| ||||
C、a
| ||||
D、a
|
若x>y>1,0<a<1,那么下列各式中正确的是( )
| A、x-a>y-a |
| B、logax>logay |
| C、ax<ay |
| D、ax>ay |
下列命题中,真命题是( )
| A、空间不同三点确定一个平面 |
| B、空间两两相交的三条直线确定一个平面 |
| C、两组对边相等的四边形是平行四边形 |
| D、和同一直线都相交的三条平行线在同一平面内 |
函数y=(
)x+2+1(a>0,a≠1)图象必经过点( )
| 1 |
| a |
| A、(-1,1) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-2,2) |
若a>b,则下列不等式中恒成立的是( )
A、
| ||||
B、
| ||||
| C、a2>b2 | ||||
| D、a3>b3 |
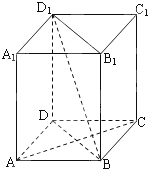 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=