题目内容
2.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期是π,且x∈(0,$\frac{π}{2}$]时,f(x)=cosx,则f(-$\frac{16π}{3}$)=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 由已知得f(-$\frac{16π}{3}$)=-f($\frac{16π}{3}$)=-f($\frac{π}{3}$)=-cos$\frac{π}{3}$,由此能求出结果.
解答 解:∵义在R上的函数f(x)既是奇函数又是周期函数,
f(x)的最小正周期是π,且x∈(0,$\frac{π}{2}$]时,f(x)=cosx,
∴f(-$\frac{16π}{3}$)=-f($\frac{16π}{3}$)=-f($\frac{π}{3}$)=-cos$\frac{π}{3}$=-$\frac{1}{2}$.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
13.直线x-y+3=0被圆x2+y2+4x-4y+6=0截得的弦长等于( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
10.执行如图所示的程序框图,若输出S的值为0.99,则判断框内可填入的条件是( )
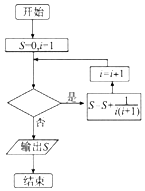

| A. | i<100 | B. | i≤100 | C. | i<99 | D. | i≤98 |
7.已知复数$\frac{a+ai}{2-ai}$为纯虚数(其中i为虚数单位),则实数a的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
14.已知定义在R上的奇函数f(x)在(0,+∞)上单调递增,f(1)=0,若f(x-2)≥0,则x的取值范围是( )
| A. | [1,3] | B. | [1,2]∪[2,3] | C. | [1,2]∪[3,+∞] | D. | [-∞,1]∪[3,+∞] |