题目内容

12．已知抛物线x2=2py（p＞0）的弦AB的中点的纵坐标为3，且|AB|的最大值为8，则p的值为（　　）
A．1B．2C．4D．8

分析 设A（x1，y1），B（x2，y2），由A、B中点的纵坐标为4，知y1+y2=6，由|AB|=y1+y2+p，弦AB的长度，可得结论．

解答 解：设A（x1，y1），B（x2，y2），
∵A、B中点的纵坐标为3，
∴y1+y2=6，
当弦AB过焦点时，|AB|取最大值，
此时|AB|=y1+y2+p=6+p=8，
∴p=2．
故选B．

点评 本题考查抛物线的性质和应用，解题时要认真审题，仔细解答，注意公式的合理运用．

练习册系列答案
相关题目
2．若${∫}_{0}^{a}$xdx=2，则常数a的值为2．
3．已知函数f（x）=a（x-1）-lnx（a∈R），g（x）=ex-x-1．
（1）求函数g（x）的单调区间；
（2）若对任意x∈[1，+∞），存在x0∈R，使得f（x）≥g（x0）成立，求a的取值范围．
20．如图是某几何体的三视图，则该几何体的体积为（　　）
A．6B．9C．12D．18
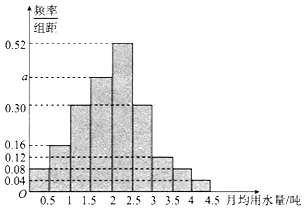7．我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．
（1）求直方图中a的值；
（2）若该市有110万居民，估计全市居民中月均用水量不低于3吨的人数，请说明理由；
（3）估计居民月均用水量的中位数（精确到0.01）
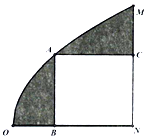17．某校一块空地的轮廓线如图所示，曲线段OM是以O为顶点，ON为对称轴且开口向右的抛物线的一段，已知ON=4（单位：百米），MN=4．现计划在该区域内围出一块矩形地块ABNC作为学生活动区域，其余阴影部分进行绿化建设，其中A在曲线段OM上，C在MN上，B在ON上．
（Ⅰ）建立适当的坐标系，求曲线段OM所在的抛物线的方程；
（Ⅱ）为降低绿化成本，试确定A的位置，使绿化建设的面积取到最小值，并求出该最小值．
4．已知复数z=a+i，a∈R，若z+$\overline{z}$=2，则复数z的共轭复数$\overline{z}$=（　　）
A．1+iB．1-iC．-1+iD．-1-i
1．已知集合A={x|-1≤x＜3}，B={2＜x≤5}，则A∩B=（　　）
A．（2，3）B．[2，3]C．（-1，5）D．[-1，5]
2．定义在R上的函数f（x）既是奇函数又是周期函数，若f（x）的最小正周期是π，且x∈（0，$\frac{π}{2}$]时，f（x）=cosx，则f（-$\frac{16π}{3}$）=（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．-$\frac{1}{2}$D．-$\frac{\sqrt{3}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网