题目内容
17.已知p:方程x2+2x+m=0无实数根,q:方程$\frac{{x}^{2}}{m-1}$+y2=1是焦点在x轴上的椭圆,若“非p”与“p且q”同时为假命题,求实数m的取值范围.分析 分别求出关于p,q成立的m的范围,根据p,q的真假,得到关于m的不等式组,解出即可.
解答 解:由p:方程无实根是真命题,
得△=4-4m<0,解得m>1;
由q:方程$\frac{x^2}{m-1}+{y^2}=1$是焦点在轴上的椭圆是真命题,
得m-1>1,解得m>2;
因为“非p”与“p且q”同时为假命题,
所以p是真命题,q是假命题,
故$\left\{\begin{array}{l}{m>1}\\{m≤2}\end{array}\right.$,解得:1<m≤2,
综上所述,m的取值范围是{m|1<m≤2}.
点评 本题考查了复合命题的判断,考查二次函数以及椭圆的性质,是一道基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
5.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
| A. | $2\frac{1}{18}$ | B. | $2\frac{1}{17}$ | C. | $2\frac{2}{17}$ | D. | $2\frac{1}{9}$ |
12.一个几何体的三视图如图所示,则该几何体的体积为( )
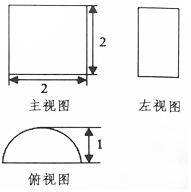

| A. | π | B. | 2π | C. | 2π+4 | D. | 3π+4 |
2.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期是π,且x∈(0,$\frac{π}{2}$]时,f(x)=cosx,则f(-$\frac{16π}{3}$)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
9.已知函数f(x)=cos(2x-$\frac{π}{6}$)(x∈R),下列命题正确的是( )
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | B. | f(x)的图象关于点($\frac{π}{12}$,0)对称 | ||
| C. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | f(x)在区间(-$\frac{π}{3}$,$\frac{π}{12}$)上是增函数 |
6.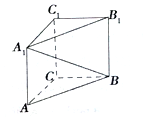 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
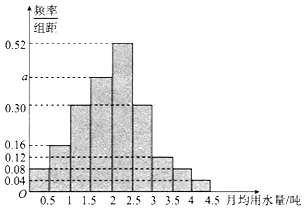 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.