题目内容
11.已知p:方程x2-2x+$\frac{1}{2}$m=0有实数根,q:方程$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{4}$=1表示焦点在x轴上的椭圆,若p且q为真命题,求实数m的取值范围.分析 分别求出关于p,q成立的m的范围,根据p且q为真命题,得到关于m的不等式组,解出即可.
解答 解:若p为真,即方程${x^2}-2x+\frac{1}{2}m=0$有解,
∴4-2m≥0,即m≤2…(3分)
若q为真,即$\frac{x^2}{m+3}+\frac{y^2}{4}=1$表示焦点在x轴上的椭圆,
∴m+3>4,即m>1…(6分)
因为p且q为真,所以p和q都为真,…(8分)
∴$\left\{\begin{array}{l}m≤2\\ m>1\end{array}\right.$,解得1<m≤2,
∴m∈(1,2].…(10分)
点评 本题考查了复合命题的判断,考查二次函数的性质以及椭圆的性质,是一道中档题.

练习册系列答案
相关题目
1.已知集合A={x|-1≤x<3},B={2<x≤5},则A∩B=( )
| A. | (2,3) | B. | [2,3] | C. | (-1,5) | D. | [-1,5] |
2.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期是π,且x∈(0,$\frac{π}{2}$]时,f(x)=cosx,则f(-$\frac{16π}{3}$)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
19.在△ABC中,D为BC上的点,AD平分∠BAC,且△ABD的面积是△ACD的面积的一半.
(Ⅰ)求$\frac{sin∠B}{sin∠C}$的值;
(Ⅱ)若∠BAC=120°,AD=1,求AC的长.
(Ⅰ)求$\frac{sin∠B}{sin∠C}$的值;
(Ⅱ)若∠BAC=120°,AD=1,求AC的长.
6.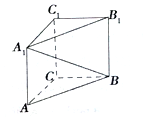 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
16.设首项为1,公比为$\frac{1}{3}$的等比数列{an}的前n项和Sn,则Sn=( )
| A. | $\frac{3-2{a}_{n}}{2}$ | B. | $\frac{2{a}_{n}-3}{2}$ | C. | $\frac{3-{a}_{n}}{2}$ | D. | $\frac{{a}_{n}-3}{2}$ |
18.已知双曲线C:mx2+ny2=1(mn<0)的一条渐近线与圆x2+y2-6x-2y+9=0相切,则C的离心率等于( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{25}{16}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |