题目内容
9.设数列{an}的前n项和记为Sn,若对任意的正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”.(1)若数列{an}的通项公式an=2n-1,判断{an}是否为“H数列”;
(2)设等差数列{an}的公差d≠0,首项a1=2d,求证:{an}是“H数列”;
(3)设点(Sn,an+1)在直线(1-q)x+y=r上,其中a1=2t>0,q≠0,若数列{an}是“H数列”,求q,r满足的条件.
分析 (1)通过n=1,a1=S1=2,然后求解数列的Sn,利用新定义判断即可.
(2)求出Sn,对任意n∈N*,存在m∈N*使Sn=am,利用新定义判断即可.
(3)n≥2时,推出an+1=qan,求出an=$\left\{\begin{array}{l}{2t,n=1}\\{p•{q}^{n-2},n≥2}\end{array}\right.$.通过q=1时,推出{an}不是“H数列”,q≠1时,求出Sn,利用新定义推出q=2,r=0,t>0的正实数.
解答 (1)解:n=1,a1=S1=1,∴Sn=$\frac{{2}^{n}-1}{2-1}$=2n-1是奇数,2m-1是偶数,∴2n-1≠2m-1,
∴{an}不是“H数列”.
(2)证明:Sn=na1+$\frac{n(n-1)}{2}$d
对任意n∈N*,存在m∈N*使Sn=am,即na1+$\frac{n(n-1)}{2}$d=a1+(m-1)d,a1=2d≠0,
∴m=2n-1+$\frac{n(n-1)}{2}$,
n,n-1是一奇一偶,∴m一定是自然数;
∴{an}是“H数列”.
(3)解:由题意可得:n≥2时(1-q)Sn+an+1=r,(1-q)Sn-1+an=r(1-q)an+an+1-an=0,
∴an+1=qan,
(1-q)×2t+a2=ra2=r+2qt-2t=p,
∴an=$\left\{\begin{array}{l}{2t,n=1}\\{p•{q}^{n-2},n≥2}\end{array}\right.$.
q=1时,an=$\left\{\begin{array}{l}{2t,n=1}\\{p,n≥2}\end{array}\right.$,
Sn=2t+(n-1)r=r不恒成立 显然{an}不是“H数列”,
q≠1时Sn=2t+$\frac{p(1-{q}^{n-1})}{1-q}$,
n=1,S1=a1,{an}是“H数列”,所以对任意n≥2时,存在m∈N*成立,
∴Sn=2t+$\frac{p}{1-q}$-$\frac{p{q}^{n-1}}{1-q}$=pqm-2,可得-$\frac{p{q}^{n-1}}{1-q}$=pqm-2,即qn-1=(q-1)qm-2,解得q=2,
∴q=2,由2t+$\frac{p}{1-q}$=0,得p=2t,
由r+2qt-2t=p,∴r+4t-2t=2t,r=0,
∴q=2,r=0,t>0的正实数.
点评 本题考查数列的应用,数列与函数相结合,考查新定义的应用,转化思想以及分析问题解决问题的能力,考查了推理能力与计算能力,属于难题.

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
| A. | 线段 | B. | 双曲线 | C. | 椭圆 | D. | 两条射线 |
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-∞,6] | D. | (-∞,6) |
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{25}{16}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
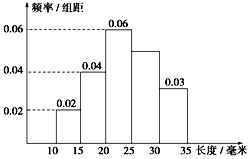 对一批零件的长度(单位:mm)进行抽样检测,检测结果的频率分布直方图如图所示.根据标准,零件长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.
对一批零件的长度(单位:mm)进行抽样检测,检测结果的频率分布直方图如图所示.根据标准,零件长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.