题目内容
14．已知定义在R上的奇函数f（x）在（0，+∞）上单调递增，f（1）=0，若f（x-2）≥0，则x的取值范围是（ ）| A． | [1，3] | B． | [1，2]∪[2，3] | C． | [1，2]∪[3，+∞] | D． | [-∞，1]∪[3，+∞] |
分析 根据函数奇偶性和单调性的关系进行求解即可．
解答 
解：∵奇函数f（x）在区间（0，+∞）单调递增，
∴函数f（x）在区间（-∞，0）上单调递增，
由f（1）=0，f（x-2）≥0，即f（x-2）≥f（1）
或f（x-2）≥f（-1），
得x-2≥1或-1≤x-2≤0，
则x≥3或1≤x≤2，
故选C．
点评 本题主要考查不等式的求解，根据函数奇偶性和单调性的关系是解决本题的关键．
练习册系列答案
相关题目
4．已知复数z=a+i，a∈R，若z+$\overline{z}$=2，则复数z的共轭复数$\overline{z}$=（ ）
| A． | 1+i | B． | 1-i | C． | -1+i | D． | -1-i |
5．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有垣厚五尺，两鼠对穿．大鼠日一尺，小鼠亦日一尺．大鼠日自倍，小鼠日自半．问几何日相逢？各穿几何？”，翻译成今天的话是：一只大鼠和一只小鼠分别从的墙两侧面对面打洞，已知第一天两鼠都打了一尺长的洞，以后大鼠每天打的洞长是前一天的2倍，小鼠每天打的洞长是前一天的一半，已知墙厚五尺，问两鼠几天后相见？相见时各打了几尺长的洞？设两鼠x 天后相遇（假设两鼠每天的速度是匀速的），则x=（ ）
| A． | $2\frac{1}{18}$ | B． | $2\frac{1}{17}$ | C． | $2\frac{2}{17}$ | D． | $2\frac{1}{9}$ |
2．定义在R上的函数f（x）既是奇函数又是周期函数，若f（x）的最小正周期是π，且x∈（0，$\frac{π}{2}$]时，f（x）=cosx，则f（-$\frac{16π}{3}$）=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
9．已知函数f（x）=cos（2x-$\frac{π}{6}$）（x∈R），下列命题正确的是（ ）
| A． | 若f（x1）=f（x2）=0，则x1-x2=kπ（k∈Z） | B． | f（x）的图象关于点（$\frac{π}{12}$，0）对称 | ||
| C． | f（x）的图象关于直线x=$\frac{π}{3}$对称 | D． | f（x）在区间（-$\frac{π}{3}$，$\frac{π}{12}$）上是增函数 |
19．在△ABC中，D为BC上的点，AD平分∠BAC，且△ABD的面积是△ACD的面积的一半．
（Ⅰ）求$\frac{sin∠B}{sin∠C}$的值；
（Ⅱ）若∠BAC=120°，AD=1，求AC的长．
（Ⅰ）求$\frac{sin∠B}{sin∠C}$的值；
（Ⅱ）若∠BAC=120°，AD=1，求AC的长．
6．
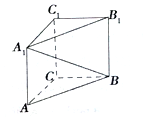如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=AC=BC=1，则异面直线A1B与AC所成角的余弦值是（ ）
如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=AC=BC=1，则异面直线A1B与AC所成角的余弦值是（ ）| A． | -$\frac{\sqrt{3}}{3}$ | B． | -$\frac{\sqrt{2}}{3}$ | C． | $\frac{\sqrt{2}}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |