题目内容
7.已知复数$\frac{a+ai}{2-ai}$为纯虚数(其中i为虚数单位),则实数a的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
分析 利用复数的运算法则、纯虚数的定义即可得出.
解答 解:复数$\frac{a+ai}{2-ai}$=$\frac{a(1+i)(2+ai)}{(2-ai)(2+ai)}$=$\frac{a(2-a)+a(2+a)i}{4+{a}^{2}}$为纯虚数(其中i为虚数单位),
则$\frac{a(2-a)}{4+{a}^{2}}$=0,$\frac{a(2+a)}{4+{a}^{2}}$≠0,
解得a=2.
故选:C.
点评 本题考查了复数的运算法则、纯虚数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
2.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期是π,且x∈(0,$\frac{π}{2}$]时,f(x)=cosx,则f(-$\frac{16π}{3}$)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
12.已知平面区域Ω={(x,y)|x>0,y>0,x+y<2},A={(x,y)|x<1,y<1,x+y>1},若在区间Ω内随机投一点P,则点P落入区域A的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
19.在△ABC中,D为BC上的点,AD平分∠BAC,且△ABD的面积是△ACD的面积的一半.
(Ⅰ)求$\frac{sin∠B}{sin∠C}$的值;
(Ⅱ)若∠BAC=120°,AD=1,求AC的长.
(Ⅰ)求$\frac{sin∠B}{sin∠C}$的值;
(Ⅱ)若∠BAC=120°,AD=1,求AC的长.
16.设首项为1,公比为$\frac{1}{3}$的等比数列{an}的前n项和Sn,则Sn=( )
| A. | $\frac{3-2{a}_{n}}{2}$ | B. | $\frac{2{a}_{n}-3}{2}$ | C. | $\frac{3-{a}_{n}}{2}$ | D. | $\frac{{a}_{n}-3}{2}$ |
14.若函数f(x)=sin2x+4cosx+ax在R上单调递减,则实数a的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-∞,6] | D. | (-∞,6) |
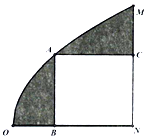 某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.
某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.