题目内容
8.定积分${∫}_{0}^{\frac{π}{3}}$(x2+sinx)dx的值为( )| A. | $\frac{{π}^{3}}{81}$+$\frac{1}{2}$ | B. | $\frac{{π}^{3}}{81}$-$\frac{1}{2}$ | C. | $\frac{2π}{3}$-$\frac{1}{2}$ | D. | $\frac{2π}{3}$+$\frac{1}{2}$ |
分析 根据定积分的运算,即可求得答案.
解答 解:${∫}_{0}^{\frac{π}{3}}$(x2+sinx)dx=($\frac{1}{3}$x3-cosx)${丨}_{0}^{\frac{π}{3}}$=($\frac{{π}^{3}}{81}$-$\frac{1}{2}$)-(0-1)=$\frac{{π}^{3}}{81}$+$\frac{1}{2}$,
${∫}_{0}^{\frac{π}{3}}$(x2+sinx)dx=$\frac{{π}^{3}}{81}$+$\frac{1}{2}$,
故选B.
点评 本题考查定积分的运算,考查计算能力,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
20.已知直线且l:mx+y+3m-$\sqrt{3}$=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,若|AB|=2$\sqrt{3}$,则|CD|=( )
| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
 如图,已知直角梯形ABCD所在的平面垂直于平面ABE,∠EAB=∠ABC=90°,∠DAB=60°,AB=AD=AE,P为线段BE的中点.
如图,已知直角梯形ABCD所在的平面垂直于平面ABE,∠EAB=∠ABC=90°,∠DAB=60°,AB=AD=AE,P为线段BE的中点.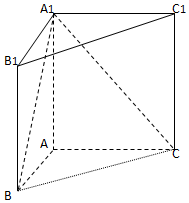 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.