题目内容
17.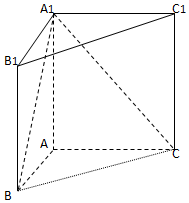 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.(Ⅰ)证明:AB⊥A1C;
(Ⅱ)求二面角A-A1C-B的正切值.
分析 (Ⅰ)三棱柱ABC-A1B1C1为直三棱柱,可得AB⊥A1A,在△ABC中,AB=1,AC=$\sqrt{3}$,∠ABC=60°.由正弦定理得:∠ACB=30°,∠BAC=90°.AB⊥AC,再利用线面垂直的判定与性质定理即可证明AB⊥A1C.
(Ⅱ)作AD⊥A1C交A1C于D,连接BD,由三垂线定理可得BD⊥A1C.可得∠ADB为二面角A-A1C-B的平面角,利用直角三角形的边角关系即可得出.
解答 (Ⅰ)证明:∵三棱柱ABC-A1B1C1为直三棱柱,
∴AB⊥A1A,
在△ABC中,AB=1,AC=$\sqrt{3}$,∠ABC=60°.
由正弦定理得:$\frac{1}{sin∠ACB}$=$\frac{\sqrt{3}}{sin6{0}^{°}}$,∴sin∠ACB=$\frac{1}{2}$,∠ACB为锐角.
∴∠ACB=30°,
∴∠BAC=90°.
即AB⊥AC,又AA1∩AC=A,
∴AB⊥侧面ACC1A1.
又∵AC1?侧面ACC1A1.
∴AB⊥A1C.
(Ⅱ)作AD⊥A1C交A1C于D,连接BD,
由三垂线定理可得BD⊥A1C.
所以∠ADB为二面角A-A1C-B的平面角,
在Rt△AA1C中,$AD=\frac{{{A_1}A•AC}}{{{A_1}C}}=\frac{{\sqrt{6}}}{2}$,
在Rt△BAD中,$tan∠ADB=\frac{AB}{AD}=\frac{{\sqrt{6}}}{3}$,
∴二面角A-A1C-B的正切值为$\frac{{\sqrt{6}}}{3}$.
点评 本题考查了空间位置关系、线面垂直的判定与性质、空间角、正弦定理、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
7.设A,B分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右顶点,P是双曲线C上异于A,B的任一点,设直线AP,BP的斜率分别为m,n,则$\frac{2a}{b}$+ln|m|+ln|n|取得最小值时,双曲线C的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{6}$ |
8.定积分${∫}_{0}^{\frac{π}{3}}$(x2+sinx)dx的值为( )
| A. | $\frac{{π}^{3}}{81}$+$\frac{1}{2}$ | B. | $\frac{{π}^{3}}{81}$-$\frac{1}{2}$ | C. | $\frac{2π}{3}$-$\frac{1}{2}$ | D. | $\frac{2π}{3}$+$\frac{1}{2}$ |
5.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的右焦点为F,上顶点为A,若直线AF与圆O:${x^2}+{y^2}=\frac{{3{a^2}}}{16}$相切,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$或$\frac{{\sqrt{3}}}{2}$ |
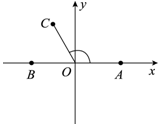 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.