题目内容
3.若a>b>c,且a+b+c=0,则$\frac{a}{c}$的取值范围是$(-2,-\frac{1}{2})$.分析 a+b+c=0,可得a>0,c<0,b=-a-c,根据a>b>c,可得-a-c<a,$\frac{c}{a}$>-2.将b=-a-c代入b>c,得-a-c>c,可得 $\frac{c}{a}$<-$\frac{1}{2}$,即可得出.
解答 解:∵a+b+c=0,
∴a>0,c<0 ①
∴b=-a-c,且a>0,c<0
∵a>b>c
∴-a-c<a,即2a>-c ②
∴$\frac{c}{a}$>-2,
将b=-a-c代入b>c,得-a-c>c,即a<-2c ③解得 $\frac{c}{a}$<-$\frac{1}{2}$,
∴-2<$\frac{c}{a}$<-$\frac{1}{2}$.
∴-2<$\frac{a}{c}$$<-\frac{1}{2}$.
故答案为:$(-2,-\frac{1}{2})$.
点评 本题考查了不等式的性质与解法、方程的解法、转化方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1,F2,两条渐近线分别为l1,l2,过F1作F1A⊥l1于点A,过F2作F2B⊥l2于点B,O为原点,若△ABO是边长为$\sqrt{3}$的等边三角形,则双曲线的方程为( )
| A. | $\frac{x^2}{21}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{21}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{9}-\frac{y^2}{3}=1$ |
11.已知α是第三象限角,则$\frac{α}{2}$是( )
| A. | 第一象限角 | B. | 第二象限角 | ||
| C. | 第一或第四象限角 | D. | 第二或第四象限角 |
8.定积分${∫}_{0}^{\frac{π}{3}}$(x2+sinx)dx的值为( )
| A. | $\frac{{π}^{3}}{81}$+$\frac{1}{2}$ | B. | $\frac{{π}^{3}}{81}$-$\frac{1}{2}$ | C. | $\frac{2π}{3}$-$\frac{1}{2}$ | D. | $\frac{2π}{3}$+$\frac{1}{2}$ |
13.函数y=tan $\frac{x}{2}$是( )
| A. | 周期为2π的奇函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为2π的偶函数 |
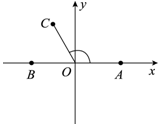 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.