题目内容
已知x,y,z>0,并且
+
+
=2,求证:
+
+
≤
.
| x2 |
| 1+x2 |
| y2 |
| 1+y2 |
| z2 |
| 1+z2 |
| x |
| 1+x2 |
| y |
| 1+y2 |
| z |
| 1+z2 |
| 2 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:构造三棱锥V-ABC中,VA,VB,VC两两垂直,高VO=1,设OA=x,OB=y,OC=z,∠OVA=α,∠OVB=β,∠OVC=γ,由条件推出得sin2α+sin2β+sin2γ=2,则cos2α+cos2β+cos2γ=1,即有
+
+
=1,再由柯西不等式,即可得证.
| 1 |
| 1+x2 |
| 1 |
| 1+y2 |
| 1 |
| 1+z2 |
解答:
 证明:在三棱锥V-ABC中,VA,VB,VC两两垂直,高VO=1,
证明:在三棱锥V-ABC中,VA,VB,VC两两垂直,高VO=1,
设OA=x,OB=y,OC=z,∠OVA=α,∠OVB=β,∠OVC=γ,
VA2=1+x2,VB2=1+y2,VC2=1+z2,
由
+
+
=2,得sin2α+sin2β+sin2γ=2,
则cos2α+cos2β+cos2γ=1,即有
+
+
=1,
由柯西不等式(
+
+
)(
+
+
)
≥(
•
+
•
+
•
)2,
则
+
+
≤
成立.
 证明:在三棱锥V-ABC中,VA,VB,VC两两垂直,高VO=1,
证明:在三棱锥V-ABC中,VA,VB,VC两两垂直,高VO=1,设OA=x,OB=y,OC=z,∠OVA=α,∠OVB=β,∠OVC=γ,
VA2=1+x2,VB2=1+y2,VC2=1+z2,
由
| x2 |
| 1+x2 |
| y2 |
| 1+y2 |
| z2 |
| 1+z2 |
则cos2α+cos2β+cos2γ=1,即有
| 1 |
| 1+x2 |
| 1 |
| 1+y2 |
| 1 |
| 1+z2 |
由柯西不等式(
| x2 |
| 1+x2 |
| y2 |
| 1+y2 |
| z2 |
| 1+z2 |
| 1 |
| 1+x2 |
| 1 |
| 1+y2 |
| 1 |
| 1+z2 |
≥(
| x | ||
|
| 1 | ||
|
| y | ||
|
| 1 | ||
|
| z | ||
|
| 1 | ||
|
则
| x |
| 1+x2 |
| y |
| 1+y2 |
| z |
| 1+z2 |
| 2 |
点评:本题考查不等式的证明,考查运用柯西不等式证明不等式,但必须构造三棱锥证得一个等式,具有一定的难度.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
“中华人民共和国个人所得税法”第六条规定,公民全月工资,薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
某人今年一月份应纳此项税款为403元,那么他当月工资的工资,薪金所得为( )
| 全月应纳税所得额 | 税率 |
| 不超过1500元部分 | 3% |
| 超过1500不超过4500元部分 | 10% |
| 超过4500元至9000元部分 | 20% |
| 超过9000元至35000元部分 | 25% |
| … | … |
| A、8290元 |
| B、7765元 |
| C、7540元 |
| D、6790元 |
函数f(x)=lnx-
ax2+x有极值且极值大于0,则a的取值范围是( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(0,2) |
| D、(3,4) |
已知双曲线的中心在原点,焦点在x轴上,一条渐进线方程是y=
x,那么它的离心率是( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
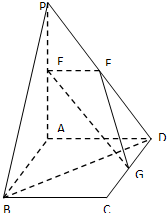 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F,G分别是线段PA、PD、CD的中点.