Question

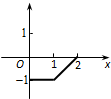
已知f（x）的图象如图，则f（x）的解析式为

 

．

Answer 1

考点：函数解析式的求解及常用方法

专题：函数的性质及应用

分析：当0≤x≤1时，函数的图象是平行于x轴的线段，故f（x）=-1；
当1＜x≤2时，函数的图象是过点（1，-1）、（2，0）的线段，设f（x）=kx+b，用待定系数法解出k、b．

解答： 解：当0≤x≤1时，函数的图象是平行于x轴的线段，故f（x）=-1；
当1＜x≤2时，函数的图象是过点（1，-1）、（2，0）的线段，
设f（x）=kx+b，∴

-1=k+b 0=2k+b

，解得k=1，b=-2，故f（x）=x-2；
∴f(x)=

-1  0≤x≤1 x-2   1＜x≤2

．
故答案为：f（x）=

-1，0≤x≤1 x-2，1＜x≤2

点评：本题主要考查根据图象求函数的解析式，如果知道函数的类别，待定系数法是常用的方法；此外，函数的表达式因自变量取值的不同而不同时，应分段表示．