Question

已知变量x，y满足约束条件

x-y≤0 x≥1 y≤2

，若该不等式组表示的平面区域被直线x+y+m=0分成面积相等的两部分，则m的值为

 

．

Answer 1

考点：二元一次不等式（组）与平面区域

专题：不等式的解法及应用

分析：先根据约束条件画出可行域，求出可行域顶点的坐标，再利用其几何意义求出答案来．

解答： 解：变量x，y满足约束条件

x-y≤0 x≥1 y≤2

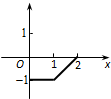
，画出约束条件表示的平面区域是△ABC如图示：
由图知，直线x+y+m=0经过点A（1，2）时，平面区域被直线x+y+m=0分为面积相等的两部分；
把x=1，y=2代入直线x+y+m=0的方程中，求得m=-3．
故答案为：-3．

点评：本题考查了用二元一次不等式组表示平面区域的问题，解题时应画出图形，结合图形解答问题，是基础题．