题目内容
已知椭圆C:
+
=1(a>b>0)经过M(
,0),N(0,1)两点.
(1)求椭圆C的标准方程;
(2)若P是该椭圆上的一个动点,F1,F2是椭圆C的两个焦点,求
•
的最大值;
(3)过点D(0,2)且斜率为k的直线l与椭圆交于不同的两点A、B,若点E(0,
),求证:对任意k2>
,
•
为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(1)求椭圆C的标准方程;
(2)若P是该椭圆上的一个动点,F1,F2是椭圆C的两个焦点,求
| PF1 |
| PF2 |
(3)过点D(0,2)且斜率为k的直线l与椭圆交于不同的两点A、B,若点E(0,
| 11 |
| 4 |
| 3 |
| 2 |
| AE |
| BE |
考点:直线与圆锥曲线的综合问题
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)由于椭圆C经过点M(
,0),N(0,1),则a=
,b=1.即可得到椭圆方程;
(2)求出焦点坐标,运用数量积的坐标公式求出
•
,再由椭圆的性质,即可得到最大值;
(3)设经过D(0,2)且斜率为k的直线l:y=kx+2,联立椭圆方程,消去y,设A(x1,y1),B(x2,y2),运用韦达定理,以及向量的坐标,运用数量积的坐标公式,化简整理,即可得到定值.
| 2 |
| 2 |
(2)求出焦点坐标,运用数量积的坐标公式求出
| PF1 |
| PF2 |
(3)设经过D(0,2)且斜率为k的直线l:y=kx+2,联立椭圆方程,消去y,设A(x1,y1),B(x2,y2),运用韦达定理,以及向量的坐标,运用数量积的坐标公式,化简整理,即可得到定值.
解答:
(1)解:由于椭圆C经过点M(
,0),N(0,1),则a=
,b=1.
故椭圆C的方程为:
+y2=1;
(2)解:由(1)知,a=
,b=1.c=1,则F1(-1,0),F2(1,0),
设P(x,y),则
•
=(-1-x,-y)•(1-x,-y)=x2+y2-1
=x2+1-
-1=
x2,
由于x∈[-
,
],当x=±
,
即P为椭圆长轴的端点时,则
•
有最大值1;
(3)证明:设经过D(0,2)且斜率为k的直线l:y=kx+2,联立椭圆方程,消去y,
得(1+2k2)x2+8kx+6=0,又k2>
,
则△=64k2-24(1+2k2)=16k2-24>0,设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
,
又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=-
,
y1+y2=(kx1+2)+(kx2+2)=k(x1+x2)+4=
,
又E(0,
),则
=(-x1,
-y1),
=(-x2,
-y2),
则有
•
=x1x2+
-
•(y1+y2)+y1y2
=
+
-
•
-
=
.
故对任意k2>
,
•
为定值.
| 2 |
| 2 |
故椭圆C的方程为:
| x2 |
| 2 |
(2)解:由(1)知,a=
| 2 |
设P(x,y),则
| PF1 |
| PF2 |
=x2+1-
| x2 |
| 2 |
| 1 |
| 2 |
由于x∈[-
| 2 |
| 2 |
| 2 |
即P为椭圆长轴的端点时,则
| PF1 |
| PF2 |
(3)证明:设经过D(0,2)且斜率为k的直线l:y=kx+2,联立椭圆方程,消去y,
得(1+2k2)x2+8kx+6=0,又k2>
| 3 |
| 2 |
则△=64k2-24(1+2k2)=16k2-24>0,设A(x1,y1),B(x2,y2),
则x1+x2=
| -8k |
| 1+2k2 |
| 6 |
| 1+2k2 |
又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=-
| 2k2-4 |
| 2k2+1 |
y1+y2=(kx1+2)+(kx2+2)=k(x1+x2)+4=
| 4 |
| 2k2+1 |
又E(0,
| 11 |
| 4 |
| AE |
| 11 |
| 4 |
| BE |
| 11 |
| 4 |
则有
| AE |
| BE |
| 121 |
| 16 |
| 11 |
| 4 |
=
| 6 |
| 1+2k2 |
| 121 |
| 16 |
| 11 |
| 4 |
| 4 |
| 2k2+1 |
| 2k2-4 |
| 2k2+1 |
| 105 |
| 16 |
故对任意k2>
| 3 |
| 2 |
| AE |
| BE |
点评:本题考查椭圆的方程和性质及运用,考查平面向量的运用,主要是数量积的坐标公式的运用,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理,化简计算,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知集合A={x|0≤x≤2},B={y|1<y<3},则A∩B=( )
| A、[1,2) |
| B、[0,3) |
| C、(1,2] |
| D、[0,3] |
已知a>b,则下列不等式中不成立的个数是( )
①a2>b2,②
<
,③
>
.
①a2>b2,②
| 1 |
| a |
| 1 |
| b |
| 1 |
| a-b |
| 1 |
| a |
| A、0 | B、1 | C、2 | D、3 |
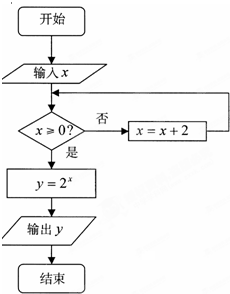 如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )
如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )