Question

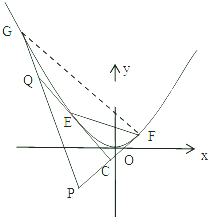抛物线y=x²的动弦为EF，分别过E，F作其切线，两切线交于C点，已知

FC

=

CP

，

CE

=

EQ

．
（1）求证：直线PQ也与抛物线相切．
（2）若PQ切抛物线于G点，求

S△GEF

S△PCQ

的值．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：（1）设E(x1，

x

2 1

)，F(x2，

x

2 2

)．y′=2x．可得切线EC与切线FC的方程．联立解得：C(

x1+x2

2

，x1x2)．
由于

FC

=

CP

，

CE

=

EQ

．可得P(x1，2x1x2-

x

2 2

)，Q(

3x1-x2

2

，2

x

2 1

-x1x2)．可得直线PQ的方程，与抛物线方程联立，化为关于x的一元二次方程，只要证明△=0即可．
（2）由于S_△PCQ=2S_△PEC=S_△PEF，可得

S△GEF

S△PCQ

=

S△GEF

S△PEF

=

hG

hP

．直线EF的方程为：y-

x

2 1

=（x₁+x₂）（x-x₁），利用点到直线的距离公式计算出点P、G到直线EF的距离之比=

hG

hP

即可．

解答： （1）证明：设E(x1，

x

2 1

)，F(x2，

x

2 2

)．
y′=2x．
∴切线EC：y-

x

2 1

=2x1(x-x1)，
切线FC：y-

x

2 2

=2x₂（x-x₂）．
联立解得：C(

x1+x2

2

，x1x2)．
∵

FC

=

CP

，

CE

=

EQ

．
∴P(x1，2x1x2-

x

2 2

)，Q(

3x1-x2

2

，2

x

2 1

-x1x2)．
k_PQ=4x₁-2x₂．
∴直线PQ的方程为：y-(2x1x2-

x

2 2

)=（4x₁-2x₂）（x-x₁）．
化为y=2(2x1-x2)x-(2x1-x2)2．
联立

y=2(2x1-x2)x-(2x1-x2)2 y=x2

．
化为x2-2(2x1-x2)x+(2x1-x2)2=0，
∴△=4(2x1-x2)2-4(2x1-x2)2=0，
因此直线PQ是抛物线的切线．
（2）解：∵S_△PCQ=2S_△PEC=S_△PEF，
∴

S△GEF

S△PCQ

=

S△GEF

S△PEF

．
∵k_EF=

x 2 1 - x 2 2

x1-x2

=x₁+x₂．
∴直线EF的方程为：y-

x

2 1

=（x₁+x₂）（x-x₁），
化为（x₁+x₂）x-y-x₁x₂=0．
∴点P、G到直线EF的距离之比=

hG

hP

=

|(2x1-x2)(x1+x2)-(2x1-x2)2-x1x2|

|x1(x1+x2)-(2x1x2- x 2 2 )-x1x2|

=2．
∴

S△GEF

S△PCQ

=

S△GEF

S△PEF

=

hG

hP

=2．

点评：本题考查了抛物线的切线、直线的方程、中点的向量形式、中点坐标公式、三角形的面积之比、点到直线的距离公式，考查了推理能力与计算能力，属于难题．