题目内容
集合A={y|y=x3,x∈[1,2]},集合B={x|lnx-ax+2>0},且A⊆B,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:先解出集合A=[1,8],由于A⊆B,所以lnx-ax+2>0,在x∈[1,8]上恒成立,然后再分离变量进行求解.
解答:
解:因为A=[1,8],又A⊆B,
所以lnx-ax+2>0,在x∈[1,8]上恒成立,即
>a在x∈[1,8]上恒成立.
令g(x)=
,x∈[1,8],
则g′(x)=-
<0,g(x)在[1,8]递减,
所以g(x)min=g(8=
,
所以a<
.
所以lnx-ax+2>0,在x∈[1,8]上恒成立,即
| lnx+2 |
| x |
令g(x)=
| lnx+2 |
| x |
则g′(x)=-
| 1+lnx |
| x2 |
所以g(x)min=g(8=
| 2+3ln2 |
| 8 |
所以a<
| 2+3ln2 |
| 8 |
点评:本题主要考察集合间的关系,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
函数y=-
的大致图象是( )
| 1 |
| x+1 |
A、 |
B、 |
C、 |
D、 |
已知集合A={x|2x>
},B={x|log2x<1},则A∩B=( )
| 1 |
| 2 |
| A、(-1,2) |
| B、(1,2) |
| C、(0,2) |
| D、(-1,1) |
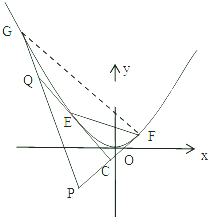 抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知
抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知