题目内容
椭圆
+
=1(a>b>o)与x轴正向交于点A,若这个椭圆上存在点P,使OP⊥AP,O为原点,求离心率e的范围.
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:向量与圆锥曲线
分析:以AO为直径的圆方程为(x-
)2+y2=
,即x2+y2-ax=0,
由
化简消去y,P、A是椭圆椭圆
+
=1与x2+y2-ax=0两个不同的公共点,
根据根与系数的关系求解.
由图形得0<m<a,0<
<a,
即b2<a2-b2,可得a2-c2<c2,得a2<2c2
a<
c,即可得到答案.
| a |
| 2 |
| a2 |
| 4 |
由
|
| x2 |
| a2 |
| y2 |
| b2 |
根据根与系数的关系求解.
由图形得0<m<a,0<
| ab2 |
| a2-b2 |
即b2<a2-b2,可得a2-c2<c2,得a2<2c2
a<
| 2 |
解答:
解:∵∠AP0=90゜,∴点P在以AO为直径的圆上,
∵O(0,0),A(a,0),
∴以AO为直径的圆方程为(x-
)2+y2=
,即x2+y2-ax=0,
由
消去y,得(b2-a2)x2+a3x-a2b2=0.
设P(m,n),
∵P、A是椭圆椭圆
+
=1与x2+y2-ax=0两个不同的公共点,
∴m+a=
,ma=
,可得m=
.
∵由图形得0<m<a,∴0<
<a,
即b2<a2-b2,可得a2-c2<c2,得a2<2c2
∴a<
c,解得椭圆离心率e=
>
=
,
又∵e∈(0,1),
∴椭圆的离心率e的取值范围为(
,1).
∵O(0,0),A(a,0),
∴以AO为直径的圆方程为(x-
| a |
| 2 |
| a2 |
| 4 |
由
|
设P(m,n),
∵P、A是椭圆椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴m+a=
| -a3 |
| b2-a2 |
| a2b2 |
| a2-b2 |
| ab2 |
| a2-b2 |
∵由图形得0<m<a,∴0<
| ab2 |
| a2-b2 |
即b2<a2-b2,可得a2-c2<c2,得a2<2c2
∴a<
| 2 |
| c |
| a |
| c | ||
|
| ||
| 2 |
又∵e∈(0,1),
∴椭圆的离心率e的取值范围为(
| ||
| 2 |
点评:本题考查了直线与椭圆的位置关系,椭圆的几何性质,运用方程组求解,难度较大.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知集合A={x|2x>
},B={x|log2x<1},则A∩B=( )
| 1 |
| 2 |
| A、(-1,2) |
| B、(1,2) |
| C、(0,2) |
| D、(-1,1) |
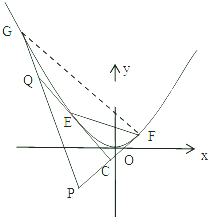 抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知
抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知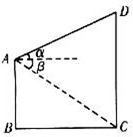 如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是
如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是