题目内容
已知函数f(x)=ax2-(a+3)x+b(a≥0,b>0),函数g(x)=lg(12-x2+4x)的定义域为B.
(1)若b=2a+1,解关于a的不等式f(-1)>8;
(2)若b=3时,关于x的不等式f(x)<0的解集为A,且A?B,求a的取值范围;
(3)若函数f(x)的一个零点在(1,2)内,一个零点在(2,3)内,求a-b的取值范围.
(1)若b=2a+1,解关于a的不等式f(-1)>8;
(2)若b=3时,关于x的不等式f(x)<0的解集为A,且A?B,求a的取值范围;
(3)若函数f(x)的一个零点在(1,2)内,一个零点在(2,3)内,求a-b的取值范围.
考点:其他不等式的解法,函数零点的判定定理
专题:不等式的解法及应用
分析:(1)若b=2a+1,关于a的不等式即 a+(a+3)+2a+1>8,由此求得a的范围.
(2)由函数g(x)的解析式求得它的定义域B=(-2,6),解关于x的不等式f(x)<0,分类讨论求得A,再结合A?B,求得a的范围.
(3)若函数f(x)的一个零点在(1,2)内,一个零点在(2,3)内,则由二次函数的性质可得
,画出可行域,求出目标函数z=a-b的最优解,可得a-b的取值范围.
(2)由函数g(x)的解析式求得它的定义域B=(-2,6),解关于x的不等式f(x)<0,分类讨论求得A,再结合A?B,求得a的范围.
(3)若函数f(x)的一个零点在(1,2)内,一个零点在(2,3)内,则由二次函数的性质可得
|
解答:
 解:(1)若b=2a+1,关于a的不等式f(-1)>8,
解:(1)若b=2a+1,关于a的不等式f(-1)>8,
即 a+(a+3)+2a+1>8,求得a>1.
(2)由函数g(x)=lg(12-x2+4x),可得 12-x2+4x>0,
求得-2<x<6,故B=(-2,6).
∵b=3,关于x的不等式f(x)<0,即 ax2-(a+3)x+3<0,即 (ax-3)(x-1)<0.
①当a=0时,求得A={x|x>1},不满足A?B.
②当0<a<3时,
>1,此时,A=(1,
),
由A?B,可得
≤6,求得 a≥
.
综合可得,
≤a<3.
③当a=3时,
=1,此时,A=∅,满足A?B.
④当a>3时,0<
<1,此时A=(
,1),满足A?B.
综合①②③④可得 a≥
.
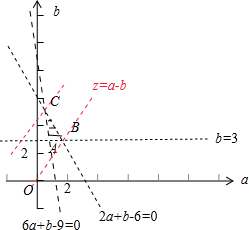
(3)若函数f(x)的一个零点在(1,2)内,一个零点在(2,3)内,则由二次函数的性质可得
,
画出可行域,如图所示:△ABC的内部区域,故当直线z=a-b经过点C(
,
)时,z=a-b取得最小值为-
,
当直线z=a-b经过点B(
,3)时,z=a-b取得最大值为-
,
故a-b的取值范围(-
,-
).
 解:(1)若b=2a+1,关于a的不等式f(-1)>8,
解:(1)若b=2a+1,关于a的不等式f(-1)>8,即 a+(a+3)+2a+1>8,求得a>1.
(2)由函数g(x)=lg(12-x2+4x),可得 12-x2+4x>0,
求得-2<x<6,故B=(-2,6).
∵b=3,关于x的不等式f(x)<0,即 ax2-(a+3)x+3<0,即 (ax-3)(x-1)<0.
①当a=0时,求得A={x|x>1},不满足A?B.
②当0<a<3时,
| 3 |
| a |
| 3 |
| a |
由A?B,可得
| 3 |
| a |
| 1 |
| 2 |
综合可得,
| 1 |
| 2 |
③当a=3时,
| 3 |
| a |
④当a>3时,0<
| 3 |
| a |
| 3 |
| a |
综合①②③④可得 a≥
| 1 |
| 2 |
(3)若函数f(x)的一个零点在(1,2)内,一个零点在(2,3)内,则由二次函数的性质可得
|
画出可行域,如图所示:△ABC的内部区域,故当直线z=a-b经过点C(
| 3 |
| 4 |
| 9 |
| 2 |
| 15 |
| 4 |
当直线z=a-b经过点B(
| 3 |
| 2 |
| 3 |
| 2 |
故a-b的取值范围(-
| 15 |
| 4 |
| 3 |
| 2 |
点评:本题主要考查对数不等式的解法,集合间的包含关系,函数零点的判定定理,以及简单的线性规划问题,体现了转化、分类讨论、数形结合的数学思想,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
已知集合A={x|2x>
},B={x|log2x<1},则A∩B=( )
| 1 |
| 2 |
| A、(-1,2) |
| B、(1,2) |
| C、(0,2) |
| D、(-1,1) |
一个正方体,它的表面涂满了红色.在它的每个面上切两刀可得27个小立方块,从中任取两个,其中恰有1个一面涂有红色,1个两面涂有红色的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知
抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知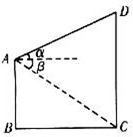 如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是
如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是