题目内容
将一枚硬币抛掷n次，求正面次数与反面次数之差x的概率分布，并求出x的期望E（x）与方差D（x）．
考点：离散型随机变量的期望与方差
专题：概率与统计
分析：设正面的次数是Y，由题意Y～B（n，0.5），E（Y）=0.5n，D（Y）=0.25n，而反面次数为n-Y，从而X=Y-（n-Y）=2Y-n，由此能求出x的期望E（x）与方差D（x）．
解答：
解：设正面的次数是Y，
由题意Y～B（n，0.5），
概率分布为P（Y=k）=
（0.5）n，k=0，1，…，n，
且E（Y）=0.5n，D（Y）=0.25n，
而反面次数为n-Y，从而X=Y-（n-Y）=2Y-n，
∴E（X）=E（2Y-n）=2E（Y）-n=2×0.5n-n=0，
D（X）=D（2Y-n）=4D（Y）=4×0.25n=n．
由题意Y～B（n，0.5），
概率分布为P（Y=k）=
| C | k n |
且E（Y）=0.5n，D（Y）=0.25n，
而反面次数为n-Y，从而X=Y-（n-Y）=2Y-n，
∴E（X）=E（2Y-n）=2E（Y）-n=2×0.5n-n=0，
D（X）=D（2Y-n）=4D（Y）=4×0.25n=n．
点评：本题考查离散型随机变量的分布列、数学期望和方差的求法，是中档题，解题时要认真审题．
练习册系列答案
53随堂测系列答案
相关题目
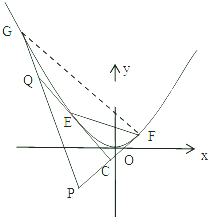抛物线y=x2的动弦为EF，分别过E，F作其切线，两切线交于C点，已知
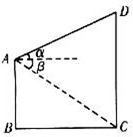如图，两座建筑物AB，CD的底部都在同一个水平面上，且AB、CD均与水平面垂直，它们的高度分别是9m和15m，从建筑物AB的顶部A看点D的仰角为α，看点C的俯角为β，已知α+β=45°，则BC的长度是