题目内容
若函数y=f(x)在(0,+∞)上是单调递增函数,则f(a2-a+3)与f(2)的大小关系是: .
考点:函数单调性的性质
专题:函数的性质及应用
分析:对a2-a+3配方,比较它与2的大小关系,根据函数y=f(x)在(0,+∞)上的单调性即可比较f(a2-a+3)与f(2)的大小关系.
解答:
解:a2-a+3=(a-
)2+
>2;
∵f(x)在(0,+∞)上是单调递增函数,∴f(a2-a+3)>f(2);
故答案为:f(a2-a+3)>f(2).
| 1 |
| 2 |
| 11 |
| 4 |
∵f(x)在(0,+∞)上是单调递增函数,∴f(a2-a+3)>f(2);
故答案为:f(a2-a+3)>f(2).
点评:考查配方法得到二次函数的最值,根据单调递增函数的定义比较两个函数值的大小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个正方体,它的表面涂满了红色.在它的每个面上切两刀可得27个小立方块,从中任取两个,其中恰有1个一面涂有红色,1个两面涂有红色的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
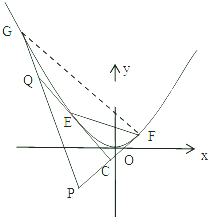 抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知
抛物线y=x2的动弦为EF,分别过E,F作其切线,两切线交于C点,已知