题目内容
已知函数f(x)=x+
,x∈[-1,0)∪(0,1].
(1)证明函数f(x)在(0,1]上的单调性.
(2)判断函数f(x)的奇偶性,并求函数f(x)在[-
,-
]上的最大值.
| 1 |
| x |
(1)证明函数f(x)在(0,1]上的单调性.
(2)判断函数f(x)的奇偶性,并求函数f(x)在[-
| 1 |
| 2 |
| 1 |
| 3 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:综合题,导数的概念及应用
分析:(1)求导数,证明f′(x)=1-
<0,即可求出函数f(x)在(0,1]上的单调性.
(2)利用奇函数的定义,即可判断;函数f(x)在[-
,-
]上单调递减,可求最大值.
| 1 |
| x2 |
(2)利用奇函数的定义,即可判断;函数f(x)在[-
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:(1)∵f(x)=x+
,
∴f′(x)=1-
,
∵x∈(0,1],
∴f′(x)=1-
<0,
∴函数f(x)在(0,1]上单调递减;
(2)f(-x)=-x-
=-f(x),
∴函数f(x)是奇函数;
函数f(x)在[-
,-
]上单调递减,
∴最大值为f(-
)=-
.
| 1 |
| x |
∴f′(x)=1-
| 1 |
| x2 |
∵x∈(0,1],
∴f′(x)=1-
| 1 |
| x2 |
∴函数f(x)在(0,1]上单调递减;
(2)f(-x)=-x-
| 1 |
| x |
∴函数f(x)是奇函数;
函数f(x)在[-
| 1 |
| 2 |
| 1 |
| 3 |
∴最大值为f(-
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查利用导数研究函数的单调性,考查函数的奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
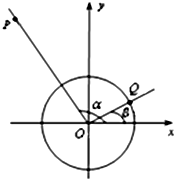 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为