题目内容
(1)等差数列{an}中,a1=2,a10=-10,求a1及Sn
(2)等比数列{an}中,a1=-1,a4=64,求q与S50.
(2)等比数列{an}中,a1=-1,a4=64,求q与S50.
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知得a10=2+9d=-10,解得d=-
,由此能求出a1=2,Sn=-110.
(2)由已知得-q3=64,由此能求出q与S50.
| 4 |
| 3 |
(2)由已知得-q3=64,由此能求出q与S50.
解答:
解:(1)∵等差数列{an}中,a1=2,n=15,a10=-10,
∴a10=2+9d=-10,解得d=-
,
∴Sn=S15=15×2+
×(-
)=-110.
∴a1=2,Sn=-110.
(2)∵等比数列{an}中,a1=-1,a4=64,
∴-q3=64,
解得q=-4,
∴S50=
=
(450-1).
∴a10=2+9d=-10,解得d=-
| 4 |
| 3 |
∴Sn=S15=15×2+
| 15×14 |
| 2 |
| 4 |
| 3 |
∴a1=2,Sn=-110.
(2)∵等比数列{an}中,a1=-1,a4=64,
∴-q3=64,
解得q=-4,
∴S50=
| -1×[1-(-4)50] |
| 1-(-4) |
=
| 1 |
| 5 |
点评:本题考查等差数列和等比数列的性质的合理运用,是基础题,解题时要认真审题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
f(x)为定义在实数上的可导函数,且f(x)<f′(x)对任意的x∈R都成立,则( )
| A、f(1)>ef(0),f(2013)>e2013f(0) |
| B、f(1)<ef(0),f(2013)>e2013f(0) |
| C、f(1)>ef(0),f(2013)<e2013f(0) |
| D、f(1)<ef(0),f(2013)<e2013f(0) |
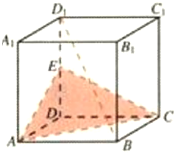 如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,
如图在正方体ABCD-A1B1C1D1中,AA1=2,E是DD1的中点,