题目内容

14．函数y=x 2cosx的导数为（　　）
A．y′=2xcosx-x 2sinxB．y′=2xcosx+x 2sinx
C．y′=x 2cosx-2xsinxD．y′=xcosx-x 2sinx

分析 根据导数的运算法则计算即可

解答 解：y=（x2）′cosx+x2（cosx）′=2xcosx-x2sinx，
故选：A

点评 本题考查了导数的运算法则，和常见函数的导数，属于基础题

练习册系列答案
相关题目
12．已知0＜a＜2，证明：$\frac{1}{a}$+$\frac{4}{2-a}$≥$\frac{9}{2}$．
13．祖暅是南北朝时代的伟大科学家，5世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积一定相等，现有以下四个几何体：图①是从圆柱中挖去一个圆锥所得的几何体；图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为（　　）
A．①②B．①③C．②④D．①④
2．若一个圆柱的轴截面是一个面积为4的正方形，则该圆柱的表面积为（　　）
A．4πB．5πC．$\frac{7π}{2}$D．6π
9．已知向量$\overrightarrow{a}$=（2sinx，cosx），$\overrightarrow{b}$=（cosx，2$\sqrt{3}$cosx），函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$
（Ι）求函数f（x）的最小正周期；
（ΙΙ） 当$x∈[0，\frac{π}{2}]$时，求函数f（x）的最大值与最小值．
19．函数f（x）=log2（x2-3x+2）的定义域为（　　）
A．（0，1）∪（2，+∞）B．（-∞，1）∪（2，+∞）C．（0，+∞）D．（1，2）
6．在锐角△ABC中，BC=1，∠B=2∠A，AC的取值范围为（　　）
A．$（{1，\sqrt{2}}）$B．$（0，\sqrt{2}]$C．$（{\sqrt{2}，\sqrt{3}}）$D．$（{1，\sqrt{3}}）$
3．已知函数f（x）=$\frac{5}{4}$sinx，x∈R．
（1）求f（$\frac{π}{6}$）的值；
（2）若f（α）=1，α∈（0，$\frac{π}{2}$），求f（2α）的值．
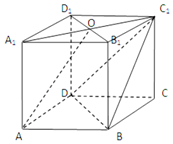4．如图，在四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD，底面ABCD为菱形，O为A1C1与B1D1的交点，已知AA1=AB=2，∠BAD=60°；
（1）求证：平面A1BC1⊥平面B1BDD1；
（2）求点O到平面BC1D的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网