题目内容
6.在锐角△ABC中,BC=1,∠B=2∠A,AC的取值范围为( )| A. | $({1,\sqrt{2}})$ | B. | $(0,\sqrt{2}]$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({1,\sqrt{3}})$ |
分析 求出A的范围,由正弦定理可得 b=2cosA,从而得到 b 的取值范围.
解答 解:在锐角△ABC中,BC=1,∠B=2∠A,
∴$\frac{π}{2}$<3 A<π,且 0<2A<$\frac{π}{2}$,
故 $\frac{π}{6}$<A<$\frac{π}{4}$,
故 $\frac{\sqrt{2}}{2}$<cosA<$\frac{\sqrt{3}}{2}$.
由正弦定理可得 $\frac{1}{sinA}$=$\frac{b}{sin2A}$,
∴b=2cosA,
∴$\sqrt{2}$<b<$\sqrt{3}$,
故选:C
点评 本题考查锐角三角形的定义,正弦定理的应用,求得 $\frac{π}{6}$<A<$\frac{π}{4}$,是解题的关键.

练习册系列答案
相关题目
5.在△ABC中,若b2+c2=a2-bc,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
14.函数y=x 2cosx的导数为( )
| A. | y′=2xcosx-x 2sinx | B. | y′=2xcosx+x 2sinx | ||
| C. | y′=x 2cosx-2xsinx | D. | y′=xcosx-x 2sinx |
1.已知数列{an}为等比数列,其中a5,a9为方程x2+2016x+9=0的二根,则a7的值( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 9 |
11.已知a,b∈R,i是虚数单位,若a+i与2-bi互为共轭复数,则$\frac{b-i}{a+i}$=( )
| A. | $\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{3}{5}$+$\frac{1}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | $\frac{3}{5}$-$\frac{1}{5}$i |
15.若双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的倾斜角是直线l:x-2y+1=0倾斜角的两倍,则双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{7}}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{3}$ |
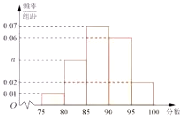 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格:
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格: