题目内容
求证：如果两两平行的三条直线都与另一条直线相交，那么这四条直线共面．
考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：先运用确定平面的条件，确定一个平面，再证明其他的直线也在这个平面中．
解答：
已知：a∥b∥c，l∩a=A，L∩b=B，L∩c=C．
求证：直线a、b、c和l共面．
证明：如图．a∥b，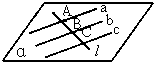
a∥b，由推论3可知，直线a与b确定一个平面，设为α．
∵l∩a=A，L∩b=B，
∴A∈a，B∈b．则A∈α，B∈α．
而A∈l，B∈l
∴由公理1可知：l?α．
∵b∥c，由推论3可知，直线b与c确定一个平面，设为β．
同理可知：l?β．
∵平面α和平面β都包含直线b与l，且l∩b=B，
∴由推论2可知经过两条相交直线，有且只有一个平面．
∴平面α与平面β重合．
∴直线a、b、c及l共面．
求证：直线a、b、c和l共面．
证明：如图．a∥b，
a∥b，由推论3可知，直线a与b确定一个平面，设为α．
∵l∩a=A，L∩b=B，
∴A∈a，B∈b．则A∈α，B∈α．
而A∈l，B∈l
∴由公理1可知：l?α．
∵b∥c，由推论3可知，直线b与c确定一个平面，设为β．
同理可知：l?β．
∵平面α和平面β都包含直线b与l，且l∩b=B，
∴由推论2可知经过两条相交直线，有且只有一个平面．
∴平面α与平面β重合．
∴直线a、b、c及l共面．
点评：本题考查了运用平面基本的公理，证明共面问题，注意思维逻辑的严密性．
练习册系列答案
相关题目
在2和20之间插入两个数，使前三个数成等比数列，后三个数成等差数列，则插入的两个数的和是（ ）
A、-4或17
| ||
B、4或17
| ||
| C、4 | ||
D、17
|
函数y=
+
的定义域是（ ）
| 1-x2 |
| x2-1 |
| A、{x|-1＜x＜1} |
| B、{x|x＜-1，或x＞1} |
| C、{x|0＜x＜1} |
| D、{-1，1} |
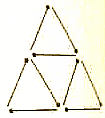用9根火柴棒搭成的图案如图所示，移动2根火柴棒，使这9根火柴棒搭成一个中心对称图形，并画出这个图形．