题目内容
设集合A={x|x2-4x-12>0},B={x||x-3|<a},且-3∈B,则A∪B= .
考点:并集及其运算
专题:集合
分析:求出集合A,B,利用-3∈B,解得a的取值范围,利用集合的并集进行运算即可得到结论.
解答:
解:∵A={x|x2-4x-12>0}={x|x>6或x<-2},-3∈B,
∴|-3-3|=6<a,
即a>6,则3-a<-3
∴B={x||x-3|<a}={x|3-a<x<3+a},
则A∪B={x|x>6或x<-2},
故答案为:{x|x>6或x<-2}
∴|-3-3|=6<a,
即a>6,则3-a<-3
∴B={x||x-3|<a}={x|3-a<x<3+a},
则A∪B={x|x>6或x<-2},
故答案为:{x|x>6或x<-2}
点评:本题主要考查集合的基本运算,根据不等式的性质求出集合A,B是解决本题的关键.

练习册系列答案
相关题目
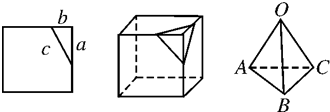
某几何体的三视图如图所示,则该几何体的体积为( )

| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
 如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.
如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.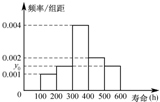 对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.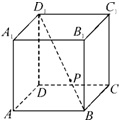 如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有
如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有