题目内容
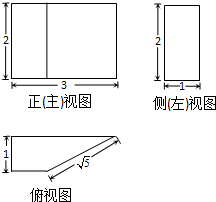
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图知几何体是一个四棱柱，四棱柱的底面是一个直角梯形，梯形的下底是3，高是1，棱柱的高为2，求出梯形的上底，然后求出棱柱的体积，得到结果．
解答：
解：由三视图知几何体是一个四棱柱，
四棱柱的底面是一个直角梯形，梯形的下底是3，斜边为
，
高是1，梯形的上底为：3-
=1，棱柱的高为2，
∴四棱柱的体积是：
×1×2=4，
故选：C．
四棱柱的底面是一个直角梯形，梯形的下底是3，斜边为
| 5 |
高是1，梯形的上底为：3-
(
|
∴四棱柱的体积是：
| 1+3 |
| 2 |
故选：C．
点评：本题考查有三视图还原几何体，本题是一个基础题，解题的过程中看清各个部分的数据，代入求体积公式得到结果．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
如图是甲，乙两名同学5次综合测评成绩的茎叶图，则乙的成绩的中位数是
一个正三棱柱的三视图如图所示，这个三棱柱的侧（左）视图的面积为6| 3 |
| A、12 | ||
| B、16 | ||
C、8
| ||
D、12
|
某几何体的俯视图是正方形，则该几何体不可能是（ ）
| A、圆柱 | B、圆锥 |
| C、三棱柱 | D、四棱柱 |
以下判断正确的是（ ）
| A、函数y=f（x）为R上的可导函数，则“f′（x0）=0”是“x0为函数f（x）极值点”的充要条件 |
| B、“a=1”是“直线ax+y-1=0与直线x+ay+1=0平行”的充要条件 |
| C、命题“在△ABC中，若A＞B，则sinA＞sinB”的逆命题为假命题 |
| D、命题“存在x∈R，x2+x-1＜0”的否定是“任意x∈R，x2+x-1＞0” |