题目内容
18.已知函数$f(x)=sinx-\frac{1}{2}$与g(x)=cos(2x+φ)$(0≤φ<\frac{π}{2})$,它们的图象有一个横坐标为$\frac{π}{6}$的交点.(Ⅰ)求φ的值;
(Ⅱ)将f(x)图象上所有点的横坐标变为原来的$\frac{1}{ω}(ω>0)$倍,得到h(x)的图象,若h(x)的最小正周期为π,求ω的值和h(x)的单调递增区间.
分析 (Ⅰ)根据f($\frac{π}{6}$)=g($\frac{π}{6}$),求得φ的值.
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律,得到h(x)的解析式,再根据正弦函数的单调性求得h(x)的增区间.
解答 解:(Ⅰ)∵函数$f(x)=sinx-\frac{1}{2}$与g(x)=cos(2x+φ)$(0≤φ<\frac{π}{2})$,它们的图象有一个横坐标为$\frac{π}{6}$的交点,
∴sin$\frac{π}{6}$-$\frac{1}{2}$=cos($\frac{π}{3}$+φ),即 cos($\frac{π}{3}$+φ)=0,∴$\frac{π}{3}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{6}$.
(Ⅱ)将函数$f(x)=sinx-\frac{1}{2}$的图象上所有点的横坐标变为原来的$\frac{1}{ω}(ω>0)$倍,得到h(x)=sin(ωx)-$\frac{1}{2}$的图象,
若h(x)的最小正周期为$\frac{2π}{ω}$=π,∴ω=2,h(x)=sin(2x)-$\frac{1}{2}$.
令2kπ-$\frac{π}{2}$≤2x≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{4}$≤x≤kπ+$\frac{π}{4}$,可得h(x)的增区间为[kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$],k∈Z.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
9.若复数$\frac{a+i}{1+2i}$(a∈R)为纯虚数,其中i为虚数单位,则a=( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
6.已知函数f(x)=sin(ωx-$\frac{π}{6}$)+$\frac{1}{2}$(ω>0),且f(a)=-$\frac{1}{2}$,f(β)=$\frac{1}{2}$,若|α-β|的最小值为$\frac{3π}{4}$,则函数的单调递增区间为( )
| A. | [-$\frac{π}{2}$+2kπ,π+2kπ],k∈Z | B. | [-$\frac{π}{2}$+3kπ,π+3kπ],k∈Z | ||
| C. | [π+2kπ,$\frac{5π}{2}$+2kπ],k∈Z | D. | [π+3kπ,$\frac{5π}{2}$+3kπ],k∈Z |
6.已知数列{an}的前n项和Sn=2an-1,则满足$\frac{a_n}{n}≤2$的正整数n的集合为( )
| A. | {1,2} | B. | {1,2,3,4} | C. | {1,2,3} | D. | {1,2,4} |
 从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: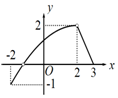


 已知函数f(x)=sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$一个周期的图象(如图),则这个函数的解析式为f(x)=$sin(2x+\frac{π}{6})$.
已知函数f(x)=sin(ωx+φ)$({ω>0,|φ|<\frac{π}{2}})$一个周期的图象(如图),则这个函数的解析式为f(x)=$sin(2x+\frac{π}{6})$.