题目内容
3.已知函数f(x),φ(x)满足关系φ(x)=f(x)•f(x+α)(其中α是常数).(1)如果α=1,f(x)=2x-1,求函数φ(x)的值域;
(2)如果α=$\frac{π}{2}$,f(x)=sinx,且对任意x∈R,存在x1,x2∈R,使得φ(x1)≤φ(x)≤φ(x2)恒成立,求|x1-x2|的最小值;
(3)如果f(x)=Asin(ωx+ϕ)(A>0,ω>0),求函数φ(x)的最小正周期(只需写出结论).
分析 (1)因为α=1,f(x)=2x-1,可得φ(x)=(2x-1)(2x+1-1)=2•(2x)2-3•2x+1,令t=2x(t>0),所以也就是求函数y=2t2-3t+1(t>0)的值域,利用二次函数的单调性即可得出.
(2)因为$α=\frac{π}{2}$,f(x)=sinx,可得$φ(x)=sinx•sin(x+\frac{π}{2})=\frac{1}{2}sin2x$,因为对任意x∈R,存在x1,x2∈R,使得φ(x1)≤φ(x)≤φ(x2)恒成立,所以φ(x1),φ(x2)应该分别为函数φ(x)在R上的最小值和最大值,所以|x1-x2|的最小值就是函数φ(x)的半周期,即可得出.
(3)T=$\frac{π}{ω}$.
解答 解:(1)因为α=1,f(x)=2x-1,
所以φ(x)=(2x-1)(2x+1-1)=2•(2x)2-3•2x+1,
令t=2x(t>0),所以也就是求函数y=2t2-3t+1(t>0)的值域,
所以φ(x)的值域为$[-\frac{1}{8},+∞)$.…(3分)
(2)因为$α=\frac{π}{2}$,f(x)=sinx,
所以$φ(x)=sinx•sin(x+\frac{π}{2})=\frac{1}{2}sin2x$,
因为对任意x∈R,存在x1,x2∈R,使得φ(x1)≤φ(x)≤φ(x2)恒成立,
所以φ(x1),φ(x2)应该分别为函数φ(x)在R上的最小值和最大值,
所以|x1-x2|的最小值就是函数φ(x)的半周期,
也就是|x1-x2|的最小值为$\frac{π}{2}$.…(7分)
(3)T=$\frac{π}{ω}$.…(9分)
点评 本题考查了抽象函数的周期性单调性与值域、三角函数的图象与性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
| A. | c>b>a | B. | b>c>a | C. | a>b>c | D. | c>a>b |
| A. | (-∞,-2)∪(0,2) | B. | (-∞,0)∪(2,+∞) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
| A. | 0<a<3 | B. | a<0或a≥3 | C. | a<0或a>3 | D. | a≤0或a≥3 |
| A. | $?x∈R,x_{\;}^2-x+\frac{1}{4}≥0$ | B. | $?x∈R,x_{\;}^2-x+\frac{1}{4}<0$ | ||
| C. | $?x∈R,x_{\;}^2-x+\frac{1}{4}≤0$ | D. | $?x∈R,{x^2}-x+\frac{1}{4}<0$ |
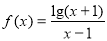 的定义域是( )
的定义域是( )