题目内容
13.若函数y=f(x)的定义域为{x|-2≤x≤3,且x≠2},值域为{y|-1≤y≤2,且y≠0},则y=f(x)的图象可能是( )| A. | 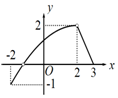 | B. |  | C. |  | D. | 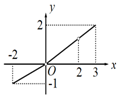 |
分析 根据函数的定义域和值域以及与函数图象之间的关系分别进行判断即可.
解答 解:A.当x=3时,y=0,∴A错误.
B.函数的定义域和值域都满足条件,∴B正确.
C.由函数的图象可知,在图象中出现了有2个函数值y和x对应的图象,∴C错误.
D.函数值域中有两个值不存在,∴函数的值域不满足条件,∴D错误.
故选:B.
点评 此题考查的是函数的定义和函数的图象问题.在解答的过程当中充分体现了函数概念的理解、一对一、多对一、定义域当中的元素必须有象等知识,同时用排除的方法解答选择题亦值得体会.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若直线y=kx+2k与曲线$y=\sqrt{1-{x^2}}$有两个不同的交点,则k的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $[{0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $[{0,\sqrt{3}})$ |
5.函数y=log2(x+2)的定义域是( )
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-2,+∞) | D. | [-2,+∞) |
1.已知函数f(x)=Asin(ωx+φ)$(A>0,|φ|<\frac{π}{2})$的图象(部分)如图所示,则$f(-\frac{1}{2})$=( )
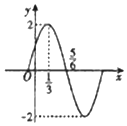

| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
1.执行如图所示的程序框图,输出S的值为( )


| A. | 6 | B. | 2log23+1 | C. | 2log23+3 | D. | log23+1 |
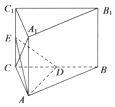 已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.
已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.