题目内容
9. 从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
从参加高二年级期中考试的学生中随机抽取60名学生,将其英语成绩分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)根据补充完整频率分布直方图估计出本次考试的平均分数、中位数;(小数点后保留一位有效数字)
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
分析 (1)计算分数在[70,80)内的频率,利用$\frac{频率}{组距}$求出小矩形的高,补出图形即可;
(2)根据频率分布直方图,计算平均分与中位数即可;
(3)根据分层抽样原理,计算各分数段内应抽取的人数即可.
解答 解:(1)分数在[70,80)内的频率为
1-(0.010+0.015+0.015+0.025+0.005)×10=1-0.7=0.3.
又$\frac{0.3}{10}$=0.03,补出的图形如下图所示;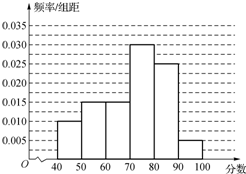
(2)根据频率分布直方图,计算平均分为:
$\overline{x}$=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
估计这次考试的平均分是71;
又0.01×10+0.015×10+0.015×10=0.4<0.5,
0.4+0.03×10=0.7>0.5,
∴中位数在[70,80)内,
计算中位数为70+$\frac{0.5-0.4}{0.03}$≈73.3;
(3)根据分层抽样原理,[40,50)分数段应抽取人数为0.10×20=2人;
[50,60)分数段应抽取人数为0.15×20=3人;
[60,70)分数段应抽取人数为0.15×20=3人;
[70,80)分数段应抽取人数为0.3×20=6人;
[80,90)分数段应抽取人数为0.25×20=5人;
[90,100]分数段应抽取人数为0.05×20=1人.
点评 本题主要考查了频率分布直方图以及平均数、中位数的计算问题,也考查了分层抽样原理的运用问题,是基础题目.

练习册系列答案
相关题目
1.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>b>0)$左右焦点分别为F1,F2,过F1做直线l与双曲线左右分别交于P,Q两点,若三角形PQF2是以Q为直角的等腰直角三角形,则e2=( )
| A. | $5-2\sqrt{2}$ | B. | $5+2\sqrt{2}$ | C. | $4+2\sqrt{2}$ | D. | $4-2\sqrt{2}$ |
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2作x轴的垂线交椭圆C于点P,若sin∠PF1F2=$\frac{1}{3}$,则( )
| A. | a=$\sqrt{2}$b | B. | a=2b | C. | a=$\sqrt{3}$b | D. | a=3b |
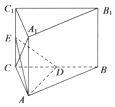 已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.
已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.