题目内容
4.双曲线$\frac{{x}^{2}}{{2}^{m}+1}$-$\frac{{y}^{2}}{{2}^{-m}+2}$=1的焦距的最小值为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
分析 由题意,2c=2$\sqrt{{2}^{m}+{2}^{-m}+3}$$≥2\sqrt{5}$,即可求出双曲线$\frac{{x}^{2}}{{2}^{m}+1}$-$\frac{{y}^{2}}{{2}^{-m}+2}$=1的焦距的最小值.
解答 解:由题意,2c=2$\sqrt{{2}^{m}+{2}^{-m}+3}$$≥2\sqrt{5}$,
∴双曲线$\frac{{x}^{2}}{{2}^{m}+1}$-$\frac{{y}^{2}}{{2}^{-m}+2}$=1的焦距的最小值为2$\sqrt{5}$,
故选B.
点评 本题考查双曲线的方程与性质,考查基本不等式的运用,比较基础.

练习册系列答案
相关题目
9.若集合A={x∈N|5+4x-x2>0},B={x|x<3},则A∩B等于( )
| A. | ∅ | B. | {1,2} | C. | [0,3) | D. | {0,1,2} |
13.命题“?x0∈R,x02+sinx0+e${\;}^{{x}_{0}}$<1”的否定是( )
| A. | ?x0∈R,x02+sinx0+e${\;}^{{x}_{0}}$>1 | B. | ?x0∈R,x02+sinx0+e${\;}^{{x}_{0}}$≥1 | ||
| C. | ?x∈R,x2+sinx+ex>1 | D. | ?x∈R,x2+sinx+ex≥1 |
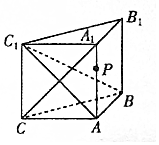 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点. 如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.
如图,PA⊥平面ABC,AB⊥BC,AB=PA=2BC=2,M为PB的中点.