题目内容
4．
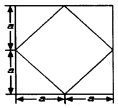已知某个几何体的正视图、侧视图、俯视图均为右图的形状，根据图中标出的尺寸（图中大正方形边长为2a），可得这个几何体的体积是（ ）| A． | $\frac{20}{3}{a^3}$ | B． | 7a3 | C． | $2\sqrt{2}{a^3}$ | D． | 5a3 |
分析 由已知中的三视图，可知该几何体是一个棱长为2a的正方体，切去了八个角所得组合体，求出每个角的体积，相减可得答案．
解答 解：由已知中的三视图，可知该几何体是一个棱长为2a的正方体，切去了八个角所得组合体，
每个角都是三条侧棱两两垂直且长度为a的棱锥，
故组合体的体积V=（2a）3-8×（$\frac{1}{3}$×$\frac{1}{2}$a2×a）=$\frac{20}{3}{a^3}$，
故选：A
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
14．为了解某地区某种农产品的年产量x（单位：吨）对价格y（单位：千元/吨）和利润z的影响，对近五年该农产品的年产量和价格统计如表：
（1）求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x-$\stackrel{∧}{a}$；
（2）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7 | 6 | 5 | 4 | 2 |
（2）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
15．下面命题：
①如果让实数a与ai对应，那么实数集与纯虚数集一一对应；
②两个复数互为共轭复数的充要条件是其积为实数；
③x=y=1是x+yi=1+i的充分非必要条件；
④0比-i大．
其中正确的命题的个数是（ ）
①如果让实数a与ai对应，那么实数集与纯虚数集一一对应；
②两个复数互为共轭复数的充要条件是其积为实数；
③x=y=1是x+yi=1+i的充分非必要条件；
④0比-i大．
其中正确的命题的个数是（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
12．设集合A={x|x≥-1}，B={x|y=ln（x-2}，则A∩∁RB=（ ）
| A． | [-1，2） | B． | [2，+∞） | C． | [-1，2] | D． | [-1，+∞） |
19．某空间几何体的三视图如图所示，则该几何体的体积是（ ）
| A． | 32 | B． | 32$\sqrt{2}$ | C． | $\frac{32}{3}$ | D． | $\frac{32}{3}$$\sqrt{2}$ |
16．
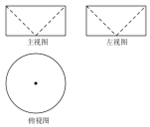如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的表面积为（ ）
如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的表面积为（ ）| A． | （$\sqrt{2}$+1）π | B． | （$\sqrt{2}$+2）π | C． | （$\sqrt{2}$+3）π | D． | （$\sqrt{2}$+4）π |
13．两相关变量满足如下关系：
两变量回归直线方程为（ ）
| x | 10 | 15 | 20 | 25 | 30 |
| Y | 1 003 | 1 005 | 1 010 | 1 011 | 1 014 |
| A． | $\stackrel{∧}{y}$=0.56$\stackrel{∧}{x}$+997.4 | B． | $\stackrel{∧}{y}$=0.63 $\stackrel{∧}{x}$-231.2 | ||
| C． | $\stackrel{∧}{y}$=50.2 $\stackrel{∧}{x}$+501.4 | D． | $\stackrel{∧}{y}$=60.4$\stackrel{∧}{x}$+400.7 |