题目内容
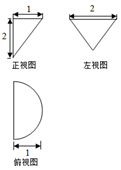
16．
如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的表面积为（ ）| A． | （$\sqrt{2}$+1）π | B． | （$\sqrt{2}$+2）π | C． | （$\sqrt{2}$+3）π | D． | （$\sqrt{2}$+4）π |
分析 由一个圆柱挖去一个圆锥所得的几何体，即可得出该几何体的表面积．
解答 解：由一个圆柱挖去一个圆锥所得的几何体，
∴该几何体的表面积S=π×12+2π×1×1+$\frac{1}{2}$×2$π×1×\sqrt{2}$=（3+$\sqrt{2}$）π．
故选：C．
点评 本题考查了圆柱与圆锥的三视图及其表面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
4．
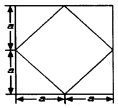已知某个几何体的正视图、侧视图、俯视图均为右图的形状，根据图中标出的尺寸（图中大正方形边长为2a），可得这个几何体的体积是（ ）
已知某个几何体的正视图、侧视图、俯视图均为右图的形状，根据图中标出的尺寸（图中大正方形边长为2a），可得这个几何体的体积是（ ）| A． | $\frac{20}{3}{a^3}$ | B． | 7a3 | C． | $2\sqrt{2}{a^3}$ | D． | 5a3 |
9．设F1，F2分别是椭圆：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，过F1倾斜角为45°的直线l与该椭圆相交于P，Q两点，且|PQ|=$\frac{4}{3}$a．则该椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{3}$ |