题目内容
13．两相关变量满足如下关系：| x | 10 | 15 | 20 | 25 | 30 |
| Y | 1 003 | 1 005 | 1 010 | 1 011 | 1 014 |
| A． | $\stackrel{∧}{y}$=0.56$\stackrel{∧}{x}$+997.4 | B． | $\stackrel{∧}{y}$=0.63 $\stackrel{∧}{x}$-231.2 | ||
| C． | $\stackrel{∧}{y}$=50.2 $\stackrel{∧}{x}$+501.4 | D． | $\stackrel{∧}{y}$=60.4$\stackrel{∧}{x}$+400.7 |
分析 把已知数据代入计算公式，验证即可．
解答 解：由题意可得$\overline{x}$=$\frac{15}{\;}$（10+15+20+25+30）=20，
$\overline{y}$=$\frac{1}{5}$（1003+1005+1010+1011+1014）=1008.6，
代入验证，可得A符合．
故选A．
点评 本题考查线性回归方程，记住公式并准确运算是解决问题的关键，属基础题．
练习册系列答案
相关题目
3．若集合A={x|x2+x-2＜0}，集合$B=\left\{{x|\frac{1}{x^2}＞1}\right\}$，则A∩B=（ ）
| A． | （-1，2） | B． | （-∞，-1）∪（1，+∞） | C． | （-1，1） | D． | （-1，0）∪（0，1） |
4．
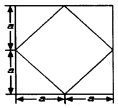已知某个几何体的正视图、侧视图、俯视图均为右图的形状，根据图中标出的尺寸（图中大正方形边长为2a），可得这个几何体的体积是（ ）
已知某个几何体的正视图、侧视图、俯视图均为右图的形状，根据图中标出的尺寸（图中大正方形边长为2a），可得这个几何体的体积是（ ）| A． | $\frac{20}{3}{a^3}$ | B． | 7a3 | C． | $2\sqrt{2}{a^3}$ | D． | 5a3 |
9．设F1，F2分别是椭圆：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，过F1倾斜角为45°的直线l与该椭圆相交于P，Q两点，且|PQ|=$\frac{4}{3}$a．则该椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{3}$ |