��Ŀ����
14��Ϊ�˽�ij����ij��ũ��Ʒ�������x����λ���֣��Լ۸�y����λ��ǧԪ/�֣�������z��Ӱ�죬�Խ������ũ��Ʒ��������ͼ۸�ͳ�������| x | 1 | 2 | 3 | 4 | 5 |
| y | 7 | 6 | 5 | 4 | 2 |
��2����ÿ�ָ�ũ��Ʒ�ijɱ�Ϊ2ǧԪ�������ũ��Ʒ��ȫ��������Ԥ������Ϊ����ʱ��������zȡ�����ֵ����������λС����
�ο���ʽ��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$��
���� ��1���ɱ��е����ݷֱ���㣬����д�����Իع鷽�̣�
��2��z=x��8.4-1.2x��=-1.2x2+6.4x�����ɵó����ۣ�
��� �⣺��1��$\overline{x}$=3��$\overline{y}$=4.8
��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{60-5��3��4.8}{55-5��{3}^{2}}$=-1.2��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$=8.4��
��y����x�����Իع鷽��$\stackrel{��}{y}$=-1.2x+8.4��
��2��z=x��8.4-1.2x��=-1.2x2+6.4x����x=2.67ʱ��������zȡ�����ֵ��
���� ���⿼���������Իع鷽�̵�Ӧ�����⣬Ҳ�������������Իع鷽��Ԥ���������⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
�����Ŀ
9����֪F1��F2�ֱ�����ԲE�����ҽ��㣬AΪ�㣬PΪ��ԲE�ϵĵ㣬��PF1Ϊֱ����Բ����F2����$|{P{F_2}}|=\frac{1}{4}|{A{F_2}}|$������ԲE��������Ϊ��������
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\frac{3}{4}$ |
19����a��0��b��0��a+b��2$\sqrt{ab}$����x+$\frac{1}{x}$��2$\sqrt{x•\frac{1}{x}}$����x+$\frac{1}{x}$��2���������������еĴ���Ϊ��������
| A�� | ��ǰ�� | B�� | Сǰ�� | C�� | ���� | D�� | ���� |
3��������A={x|x2+x-2��0}������$B=\left\{{x|\frac{1}{x^2}��1}\right\}$����A��B=��������
| A�� | ��-1��2�� | B�� | ��-�ޣ�-1���ȣ�1��+�ޣ� | C�� | ��-1��1�� | D�� | ��-1��0���ȣ�0��1�� |
4��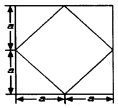 ��֪ij�������������ͼ������ͼ������ͼ��Ϊ��ͼ����״������ͼ�б���ijߴ磨ͼ�д������α߳�Ϊ2a�����ɵ���������������ǣ�������
��֪ij�������������ͼ������ͼ������ͼ��Ϊ��ͼ����״������ͼ�б���ijߴ磨ͼ�д������α߳�Ϊ2a�����ɵ���������������ǣ�������
 ��֪ij�������������ͼ������ͼ������ͼ��Ϊ��ͼ����״������ͼ�б���ijߴ磨ͼ�д������α߳�Ϊ2a�����ɵ���������������ǣ�������
��֪ij�������������ͼ������ͼ������ͼ��Ϊ��ͼ����״������ͼ�б���ijߴ磨ͼ�д������α߳�Ϊ2a�����ɵ���������������ǣ�������| A�� | $\frac{20}{3}{a^3}$ | B�� | 7a3 | C�� | $2\sqrt{2}{a^3}$ | D�� | 5a3 |