题目内容
15.已知函数$f(x)=\sqrt{3}sinxcosx+{cos^2}x+\frac{3}{2}$.(1)当$x∈[{-\frac{π}{6},\frac{π}{3}}]$时,讨论函数y=f(x)的单调性;
(2)已知ω>0,函数$g(x)=f(\frac{ωx}{2}-\frac{π}{12})$,若函数g(x)在区间$[{-\frac{2π}{3},\frac{π}{6}}]$上是增函数,求ω的最大值.
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦的定义域和值域求得f(x)的单调性.
(2)利用正弦函数的单调性、定义域和值域,求得ω的范围,可得ω的最大值.
解答 解:(1)$f(x)=\frac{{\sqrt{3}}}{2}sin2x+\frac{1+cos2x}{2}+\frac{3}{2}=sin({2x+\frac{π}{6}})+2$.
∵$x∈[{-\frac{π}{6},\frac{π}{3}}]$,∴$2x+\frac{π}{6}∈[{-\frac{π}{6},\frac{5π}{6}}]$,
所以,$-\frac{π}{6}≤2x+\frac{π}{6}≤\frac{π}{2}$,即$-\frac{π}{6}≤x≤\frac{π}{6}$时,y=f(x)增,
$\frac{π}{2}≤2x+\frac{π}{6}≤\frac{5π}{6}$,即$\frac{π}{6}≤x≤\frac{π}{3}$时,y=f(x)减,
∴函数y=f(x)在$[-\frac{π}{6},\frac{π}{6}]$上增,在$[\frac{π}{6},\frac{π}{3}]$上减.…(6分)
(2)$g(x)=sin(2(\frac{ωx}{2}-\frac{π}{12})+\frac{π}{6})+2$=sin(ωx)+2,
要使g(x)在$[-\frac{2π}{3},\frac{π}{6}]$上增,只需$-\frac{π}{2ω}≤-\frac{2π}{3}$,即$ω≤\frac{3}{4}$,
所以ω的最大值为$\frac{3}{4}$.…(12分)
点评 本题主要考查三角恒等变换,正弦函数的单调性、定义域和值域,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
6.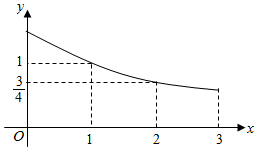 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )| A. | [-2,1] | B. | [-3,-2]∪(0,3] | C. | [-2,0]∪(1,4] | D. | [-3,0]∪[2,5] |
10.要得到函数y=sin2x的图象,只需将函数y=cos2x的图象上的所有点沿x轴( )
| A. | 向右平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向左平移$\frac{π}{2}$个单位长度 |
20.直线(tan$\frac{π}{3}$)•x+y+1=0的倾斜角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
10.已知函数f(x)=loga(1-ax)(a>0,a≠1),则不等式f(x)>f-1(1)的解为( )
| A. | (-1,0) | B. | (0,1] | C. | (0,1) | D. | (1,+∞) |