题目内容
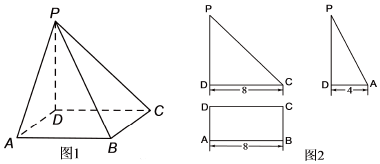
6.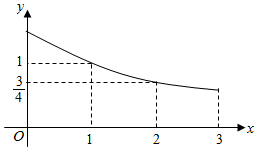 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1的取值范围是( )| A. | [-2,1] | B. | [-3,-2]∪(0,3] | C. | [-2,0]∪(1,4] | D. | [-3,0]∪[2,5] |
分析 由图象可知,当x∈(0,3]时,f(x)单调递减,当x∈[-3,0)时,f(x)单调递减,分别利用函数的图象,结合不等式f(x)≥2x-1,即可得出结论.
解答 解:由图象可知,x=0时,2x-1=0,∴f(x)≥0,成立;
当x∈(0,3]时,f(x)单调递减,
当0<x≤1时,f(x)>1,2x-1≤1,满足不等式f(x)≥2x-1;
当1<x<3时,f(x)<1,1<2x-1<7,不满足不等式f(x)≥2x-1;
∵函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,
∴当x∈[-3,0)时,f(x)单调递减,
当-3<x≤-2时,-$\frac{3}{4}$≤f(x)<0,-$\frac{7}{8}$<2x-1≤-$\frac{3}{4}$,满足不等式f(x)≥2x-1;
当x>-2时,f(x)<-$\frac{3}{4}$,2x-1>-$\frac{3}{4}$,不满足不等式f(x)≥2x-1;
∴满足不等式f(x)≥2x-1 的x的取值范围是[-3,-2]∪[0,1],
故选:B.
点评 本题考查不等式的解法,考查数形结合的数学思想,考查学生分析解决问题的能力,正确运用函数的图象是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.命题:?x∈R,x2+x-1≥0的否定是( )
| A. | ?x0∈R,x02+x0-1≥0 | B. | ?x0∈R,x02+x0-1<0 | ||
| C. | ?x∈R,x2+x-1≤0 | D. | ?x∈R,x2+x-1<0 |
14.若函数f(x)=tan(ωx-$\frac{π}{3}$)(ω>0)的最小正周期为$\frac{π}{2}$,则函数f(x)的一个单调递增区间是( )
| A. | (-$\frac{π}{6}$,$\frac{π}{12}$) | B. | ($\frac{π}{4}$,$\frac{7π}{12}$) | C. | ($\frac{π}{3}$,$\frac{5π}{6}$) | D. | (-$\frac{7π}{12}$,-$\frac{π}{12}$) |
18.已知a=${∫}_{0}^{1}$$\sqrt{x}$dx,b=${∫}_{0}^{1}$xdx,c=${∫}_{0}^{1}$x2dx,则a,b,c的大小关系是( )
| A. | c<b<a | B. | a<c<b | C. | b<a<c | D. | c<a<b |