题目内容
已知函数f(x)=x2+alnx.
(1)当a=1时,求函数f(x)的单调区间和极值;
(2)若f(x)在[1,+∞)上是单调增函数,求实数a的取值范围.
(1)当a=1时,求函数f(x)的单调区间和极值;
(2)若f(x)在[1,+∞)上是单调增函数,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的概念及应用
分析:(1)先求出函数的导数,得出f′(x)=2x+
>0,从而判断函数的单调性和极值,(2)由f′(x)=2x+
,且f(x)在[1,+∞)上是单调增函数,解不等式从而求出a的范围.
| 1 |
| x |
| a |
| x |
解答:
解:(1)a=1时:f(x)=x2+lnx,(x>0),
∴f′(x)=2x+
>0,
∴f(x)在(0,+∞)上单调递增,f(x)无极值;
(2)∵f′(x)=2x+
,
若f(x)在[1,+∞)上是单调增函数,
则:f′(1)=2+a≥0,
∴a≥-2.
∴f′(x)=2x+
| 1 |
| x |
∴f(x)在(0,+∞)上单调递增,f(x)无极值;
(2)∵f′(x)=2x+
| a |
| x |
若f(x)在[1,+∞)上是单调增函数,
则:f′(1)=2+a≥0,
∴a≥-2.
点评:本题考察了函数的单调性,极值问题,导数的应用问题,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
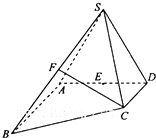 如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC=
如图,在四棱锥S-ABCD中,己如AB∥DC,AB⊥AD,△SAD是正三角形,AD=AB=2DC=2,SC= 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.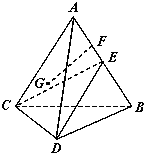 如图,在四面体ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,在四面体ABCD中,BC=AC,AD=BD,E是AB的中点.