题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的图象在y轴上的截距为1,它在y轴右侧的第一最大值点和最小值点分别为(x0,2)和(x0+3π,-2).
(1)求f(x)的解析式;
(2)将f(x)图象上所有点的横坐标缩短到原来的
,然后再将所得图象向右平移
个单位长度,得到函数g(x)的图象,写出g(x)的解析式.
| π |
| 2 |
(1)求f(x)的解析式;
(2)将f(x)图象上所有点的横坐标缩短到原来的
| 2 |
| 3 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:先根据函数的最大和最小值求得A,进而根据最高点与最低点横坐标之间的距离求得函数的最小正周期,继而求得ω,把(0,1)点代入函数解析式求得φ.
(2)利用三角函数图象平移的法则求得g(x)的图象的解析式.
(2)利用三角函数图象平移的法则求得g(x)的图象的解析式.
解答:
解:(1)∵ymax=2,ymin=-2,
∴A=2,
∵T=(x0+3π)-x0=3π,
∴
=6π,解得ω=
,
∵f(0)=2sinφ=1,
∴sinφ=
,
∵|φ|<
,
∴φ=
,
∴f(x)=3sin(
x+
).
(2)将y=2sin(
x+
)图象上的所有点横坐标缩短到原来的
,得y=2sin(
x+
)的图象,
然后将所得图象向右平移
个单位长度,得到函数y=2sin
的图象,它对应的函数即为g(x).
∴A=2,
∵T=(x0+3π)-x0=3π,
∴
| 2π |
| ω |
| 1 |
| 3 |
∵f(0)=2sinφ=1,
∴sinφ=
| 1 |
| 2 |
∵|φ|<
| π |
| 2 |
∴φ=
| π |
| 6 |
∴f(x)=3sin(
| 1 |
| 3 |
| π |
| 6 |
(2)将y=2sin(
| 1 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
然后将所得图象向右平移
| π |
| 3 |
| x |
| 2 |
点评:本题主要考查了三角函数图象与性质,三角函数图象的平移变换.考查了学生对三角函数图象的理解和应用.

练习册系列答案
相关题目
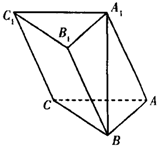 如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.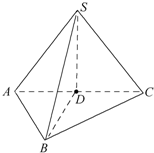 已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.
已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.