题目内容
已知数列{an}的通项公式an=(3-2n)(
)n,求数列{an}的前n项和Sn.
| 1 |
| 2 |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:利用错位相减法即可求出数列{an}的前n项和Sn
解答:
解:∵an=(3-2n)(
)n,
∴Sn=1•(
)1-1•(
)2-3•(
)3+…+(3-2n)•(
)n,①
Sn=1•(
)2-1•(
)3-3•(
)4+…+(3-2n)•(
)n+1,②
①-②得
Sn=
-2•(
)2-2•(
)3-2•(
)4-…-2(
)n-(3-2n)•(
)n+1
=
-2•
-(3-2n)•(
)n+1=
-1+(
)n-2-(3-2n)•(
)n+1,
则Sn=-1+(
)n-3-(3-2n)•(
)n.
| 1 |
| 2 |
∴Sn=1•(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则Sn=-1+(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查数列求和,利用错位相减法是解决本题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图,M,N分别是四面体OABC的边OA,BC的中点,E是MN的三等分点,且
如图,M,N分别是四面体OABC的边OA,BC的中点,E是MN的三等分点,且| NE |
| NM |
| 1 |
| 3 |
| OA |
| OB |
| OC |
| OE |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
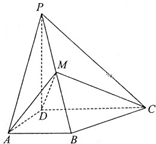 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=2,PD=