题目内容
已知集合A={x|2x<8},B={x|x2-2x-8<0},C={x|a<x<a+1}.
(Ⅰ)求集合A∩B;
(Ⅱ)若C⊆B,求实数a的取值范围.
(Ⅰ)求集合A∩B;
(Ⅱ)若C⊆B,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:(I)解指数不等式求出A,解二次不等式求出B,进而可得集合A∩B;
(Ⅱ)若C⊆B,则
,解不等式组可得实数a的取值范围.
(Ⅱ)若C⊆B,则
|
解答:
解:(Ⅰ)由2x<8,得2x<23,x<3.(3分)
解不等式x2-2x-8<0,得(x-4)(x+2)<0,
所以-2<x<4.(6分)
所以A={x|x<3},B={x|-2<x<4},
所以A∩B={x|-2<x<3}.(9分)
(Ⅱ)因为C⊆B,
所以
(11分)
解得-2≤a≤3.
所以,实数a的取值范围是[-2,3].(13分)
解不等式x2-2x-8<0,得(x-4)(x+2)<0,
所以-2<x<4.(6分)
所以A={x|x<3},B={x|-2<x<4},
所以A∩B={x|-2<x<3}.(9分)
(Ⅱ)因为C⊆B,
所以
|
解得-2≤a≤3.
所以,实数a的取值范围是[-2,3].(13分)
点评:本题考查的知识点是集合的包含关系判断及应用,集合的交集运算,解不等式,难度不大,属于基础题.

练习册系列答案
相关题目
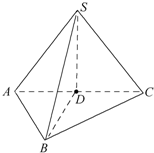 已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.
已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.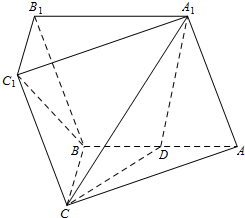 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,且∠A1AB=60°,AC=BC,D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,且∠A1AB=60°,AC=BC,D是AB的中点.