题目内容
已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|-2≤x≤1}.
(Ⅰ)求a的值;
(Ⅱ)若|f(x)-2f(
)|≤k恒成立,求k的取值范围.
(Ⅰ)求a的值;
(Ⅱ)若|f(x)-2f(
| x |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)利用绝对值不等式的解集,讨论绝对值不等式中变量a,即可求a的值;
(Ⅱ)推出f(x)-2f(
)的表达式,利用函数恒成立,直接求k的取值范围.
(Ⅱ)推出f(x)-2f(
| x |
| 2 |
解答:
解:(Ⅰ)由|ax+1|≤3,得-4≤ax≤2,
又f(x)≤3的解集为{x|-2≤x≤1}.
∴当a≤0时,不合题意;
当a>0时,-
≤x≤
,
得a=2.
(Ⅱ)记h(x)=f(x)-2f(
),
则h(x)=
,
∴|h(x)|≤1
因此k≥1.
又f(x)≤3的解集为{x|-2≤x≤1}.
∴当a≤0时,不合题意;
当a>0时,-
| 4 |
| a |
| 2 |
| a |
得a=2.
(Ⅱ)记h(x)=f(x)-2f(
| x |
| 2 |
则h(x)=
|
∴|h(x)|≤1
因此k≥1.
点评:本题考查绝对值不等式的解法,考查转化思想以及计算能力.

练习册系列答案
相关题目
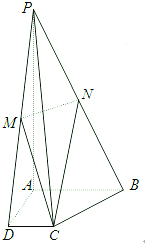 如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1, 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,