题目内容
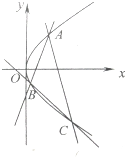 已知抛物线C:y2=2px(p>0)的焦点为F(2,0)
已知抛物线C:y2=2px(p>0)的焦点为F(2,0)(Ⅰ)求抛物线的标准方程;
(Ⅱ)抛物线C在x轴上方一点A的横坐标为2,过点A作两条倾斜角互补的直线,与曲线C的另一个交点分别为B,C,求证:直线BC的斜率为定值.
考点:抛物线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据已知中抛物线C:y2=2px(p>0)的焦点为F(2,0),求出p值,可求抛物线的标准方程;
(Ⅱ)设出直线PA、PB的方程与椭圆方程联立,求出A,B的坐标,利用斜率公式,即可证明直线AB的斜率为定值.
(Ⅱ)设出直线PA、PB的方程与椭圆方程联立,求出A,B的坐标,利用斜率公式,即可证明直线AB的斜率为定值.
解答:
解:(Ⅰ)∵抛物线C:y2=2px(p>0)的焦点为F(2,0),
∴
=2,
解得:p=4,
故抛物线C的标准方程为:y2=8x;
(Ⅱ)∵点A的横坐标为2,
故A点的坐标为(2,4),设A(x1,y1),B(x2,y2),
由已知设PA:m(y-4)=x-2,即:x=my-4m+2,
代入抛物线的方程得:y2=8(my-4m+2),即y2-8my+32m-16=0,
则:y1+4=8m,故:y1=8m-4,
设PB:-m(y-4)=x-2,即:x=-my+4m+2…(6分)
同理可得:y2=-8m-4,…(10分)
直线AB的斜率kAB=
=
=-1,
所以:直线AB的斜率为定值. …(12分)
∴
| p |
| 2 |
解得:p=4,
故抛物线C的标准方程为:y2=8x;
(Ⅱ)∵点A的横坐标为2,
故A点的坐标为(2,4),设A(x1,y1),B(x2,y2),
由已知设PA:m(y-4)=x-2,即:x=my-4m+2,
代入抛物线的方程得:y2=8(my-4m+2),即y2-8my+32m-16=0,
则:y1+4=8m,故:y1=8m-4,
设PB:-m(y-4)=x-2,即:x=-my+4m+2…(6分)
同理可得:y2=-8m-4,…(10分)
直线AB的斜率kAB=
| y1-y2 |
| x1-x2 |
| 16m |
| -16m |
所以:直线AB的斜率为定值. …(12分)
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查直线的斜率公式,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
相关题目
若向量
,
都为单位向量,则
与
一定满足( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
| C、夹角为0 | ||||||||
D、(
|
在△ABC中,向量
可以表示为①
-
;②
-
;③
+
;④
-
.( )
| BC |
| AB |
| AC |
| AC |
| AB |
| BA |
| AC |
| BA |
| CA |
| A、①②③ | B、①③④ |
| C、②③④ | D、①②④ |
 已知|
已知|