题目内容
袋中有8个白球,2个黑球,从中随机连续摸取3次,每次取1个球,求:
(1)不放回抽样时,摸出2个白球,1个黑球的概率.
(2)有放回时,摸出2个白球,一个黑球的概率.
(1)不放回抽样时,摸出2个白球,1个黑球的概率.
(2)有放回时,摸出2个白球,一个黑球的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)不放回时,求出基本事件数,计算对应的概率;
(2)有放回时,求出基本事件数,计算对应的概率即可.
(2)有放回时,求出基本事件数,计算对应的概率即可.
解答:
解:(1)不放回抽样时,从10个球中摸出3个,基本事件数是
=
=120;
其中2个白球,1个黑球的基本事件数是
•
=
•2=56;
∴它的概率为P=
=
;
(2)有放回时,从10个球中摸出3个,基本事件数是
10×10×10=1000;
其中2个白球,1个黑球的基本事件数是
8×8×2=128;
∴它的概率为P=
=
.
| C | 3 10 |
| 10×9×8 |
| 6 |
其中2个白球,1个黑球的基本事件数是
| C | 2 8 |
| C | 1 2 |
| 8×7 |
| 2 |
∴它的概率为P=
| 56 |
| 120 |
| 7 |
| 15 |
(2)有放回时,从10个球中摸出3个,基本事件数是
10×10×10=1000;
其中2个白球,1个黑球的基本事件数是
8×8×2=128;
∴它的概率为P=
| 128 |
| 1000 |
| 16 |
| 125 |
点评:本题考查了古典概型的概率计算问题,解题时应根据题意,弄清有放回与不放回对应的基本事件数,是基础题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
设等边△ABC边长为6,若
=3
,
=
,则
•
等于( )
| BC |
| BE |
| AD |
| DC |
| BD |
| AE |
A、-6
| ||
B、6
| ||
| C、-18 | ||
| D、18 |
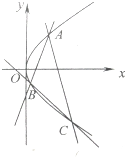 已知抛物线C:y2=2px(p>0)的焦点为F(2,0)
已知抛物线C:y2=2px(p>0)的焦点为F(2,0)