题目内容
在△ABC中,向量
可以表示为①
-
;②
-
;③
+
;④
-
.( )
| BC |
| AB |
| AC |
| AC |
| AB |
| BA |
| AC |
| BA |
| CA |
| A、①②③ | B、①③④ |
| C、②③④ | D、①②④ |
考点:向量的三角形法则
专题:平面向量及应用
分析:利用向量的三角形法则即可得出.
解答:
解:∵①
-
=
;
②
-
=
;
③
+
=
;
④
-
=
.
∴只有②③④满足条件.
故选:C.
| AB |
| AC |
| CB |
②
| AC |
| AB |
| BC |
③
| BA |
| AC |
| BC |
④
| BA |
| CA |
| BC |
∴只有②③④满足条件.
故选:C.
点评:本题考查了向量的三角形法则,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
设事件A,B,已知P(A)=
,P(B)=
,P(A∪B)=
,则A,B之间的关系一定为( )
| 1 |
| 4 |
| 1 |
| 3 |
| 7 |
| 12 |
| A、互斥事件 | B、两个任意事件 |
| C、非互斥事件 | D、对立事件 |
在△ABC中,AB=4,M为BC的中点,且AM=1,则∠BAC的最小值为( )
| A、90° | B、120° |
| C、135° | D、150° |
设等边△ABC边长为6,若
=3
,
=
,则
•
等于( )
| BC |
| BE |
| AD |
| DC |
| BD |
| AE |
A、-6
| ||
B、6
| ||
| C、-18 | ||
| D、18 |
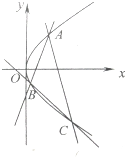 已知抛物线C:y2=2px(p>0)的焦点为F(2,0)
已知抛物线C:y2=2px(p>0)的焦点为F(2,0)