题目内容
已知函数f(x)=
(a、b为常数).
(1)若a=2,b=1,解不等式f(x-1)>0;
(2)当x∈[-1,2]时,f (x)的值域为[
,2],求a、b的值.
| x+a |
| x+b |
(1)若a=2,b=1,解不等式f(x-1)>0;
(2)当x∈[-1,2]时,f (x)的值域为[
| 5 |
| 4 |
考点:函数的值域,其他不等式的解法
专题:函数的性质及应用
分析:本题(1)利用函数解析式得到分式不等式,再转化为整式不等式,解不等式,得到本题结论;(2)利用函数的单调性,得到相应的方程,解方程组得到本题结论,本题要利用连续区间内一定有单调性的这一特征,还要根据不同的单调性情况进行分类讨论.
解答:
解析:(1)∵函数f(x)=
(a、b为常数),
∴当a=2,b=1时,f(x)=
,
∴f(x-1)=
>0,
∴x(x+1)>0,
不等式的解为:x>0或x<-1.
(2)∵函数f(x)=
(a、b为常数),
∴f(x)=1+
,
①当a>b时,f(x)在(-∞,-b]单调递减,f(x)在(-b,+∞)单调递减,
∴
,
∴
.
②当a=b时,不符合题意
③当a<b时,f(x)单调递增,
∴
,
∴
.
故所求的值为a=3,b=2或a=-4,b=-3.
| x+a |
| x+b |
∴当a=2,b=1时,f(x)=
| x+2 |
| x+1 |
∴f(x-1)=
| x+1 |
| x |
∴x(x+1)>0,
不等式的解为:x>0或x<-1.
(2)∵函数f(x)=
| x+a |
| x+b |
∴f(x)=1+
| a-b |
| x+b |
①当a>b时,f(x)在(-∞,-b]单调递减,f(x)在(-b,+∞)单调递减,
∴
|
∴
|
②当a=b时,不符合题意
③当a<b时,f(x)单调递增,
∴
|
∴
|
故所求的值为a=3,b=2或a=-4,b=-3.
点评:本题考查了分式不等式的解法和函数单调性的应用,本题难度不大,属于基础题.

练习册系列答案
相关题目
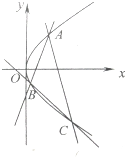 已知抛物线C:y2=2px(p>0)的焦点为F(2,0)
已知抛物线C:y2=2px(p>0)的焦点为F(2,0)