题目内容
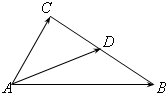已知|| p |
| 2 |
| q |
| p |
| q |
| π |
| 4 |
| AB |
| P |
| Q |
| AC |
| P |
| Q |
| AC |
| p |
| q |
| AD |
A、
| ||||
B、
| ||||
| C、7 | ||||
| D、8 |
考点：向量在几何中的应用
专题：计算题,平面向量及应用
分析：由题意，化简
2=（
（
+
））2=
（
+
）2=
（5
+2
+
-3
）2=
（6
-
）2=
（36
2+
2-12
•
）=
（36×（2
）2+32-12×2
×3×cos
）=
×9×25；从而解得．
| AD |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 4 |
| AB |
| AC |
| 1 |
| 4 |
| P |
| q |
| p |
| q |
| 1 |
| 4 |
| P |
| q |
| 1 |
| 4 |
| P |
| q |
| P |
| q |
| 1 |
| 4 |
| 2 |
| 2 |
| π |
| 4 |
| 1 |
| 4 |
解答：
解：由题意，
2=（
（
+
））2
=
（
+
）2
=
（5
+2
+
-3
）2
=
（6
-
）2
=
（36
2+
2-12
•
）
=
（36×（2
）2+32-12×2
×3×cos
）
=
×9×25；
故|
|=
=
；
故选A．
| AD |
| 1 |
| 2 |
| AB |
| AC |
=
| 1 |
| 4 |
| AB |
| AC |
=
| 1 |
| 4 |
| P |
| q |
| p |
| q |
=
| 1 |
| 4 |
| P |
| q |
=
| 1 |
| 4 |
| P |
| q |
| P |
| q |
=
| 1 |
| 4 |
| 2 |
| 2 |
| π |
| 4 |
=
| 1 |
| 4 |
故|
| AD |
|
| 15 |
| 2 |
故选A．
点评：本题考查了平面向量在几何中的应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
命题p：不等式x2+2x+a≤0的解集不是空集；命题q：函数y=（5-2a）x是增函数．若p或q为真命题，p且q为假命题，则实数a的取值范围是（ ）
| A、a≤1 | B、a＜2 |
| C、1＜a＜2 | D、a≤1或a≥2 |
在△ABC中，AB=4，M为BC的中点，且AM=1，则∠BAC的最小值为（ ）
| A、90° | B、120° |
| C、135° | D、150° |
如图所示，正方体ABCD-A1B1C1D1的棱长为1，点M、N分别是面对角线A1B和B1D1的中点．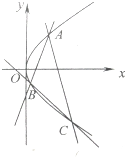
已知抛物线C：y2=2px（p＞0）的焦点为F（2，0）